Hi there.
Of course. Please find below the code that works.
If I change this line in the following program:
V_prime = grad(outputs = network(input), inputs = input, grad_outputs=torch.ones_like(input))[0]
to this:
V_prime = grad(outputs = network(input), inputs = input, create_graph = True, grad_outputs=torch.ones_like(input))[0]
the results turn out wrong. Without create_graph = True as an argument, the code is able to reproduce exactly the results I obtain from solving this PDE with a method other than neural networks.
import numpy as np
import matplotlib.pyplot as plt
import torch #PyTorch
import torch.nn as nn #PyTorch module for neural nets
from torch.autograd import grad #For taking derivatives
# Parameters
gamma = 2.0
rho = 0.04
A = 0.5
alpha = 0.36
delta = 0.05
batchSize = 100 # Batch Size
number_epochs = 50_000 # Number of epochs
kMin = 0.1 # Lower bound for state space
kMax = 10.0 # Upper bound for state space
gridSize = 10_000 # Plotting grid
# Value function initial guess
VFInitGuess = -60
# Steady state K
k_ss = (alpha*A/(rho + delta))**(1/(1-alpha))
# Set global seed
torch.manual_seed(1234)
np.random.seed(1234)
# Functions and classes
class neural_net(nn.Module): #making a class for neural networks
def __init__(self, nNeurons = 12, initGuess = 0):
super(neural_net, self).__init__()
self.linear_layer_1 = nn.Linear(1, nNeurons) #first linear layer: 1-dimensional input and 12-dimensional output
self.linear_layer_2 = nn.Linear(nNeurons, nNeurons) #second layer: 12-dimensional input and 12-dimensional output
self.linear_layer_3 = nn.Linear(nNeurons, nNeurons) #third layer: 12-dimensional input and 12-dimensional output
self.linear_layer_4 = nn.Linear(nNeurons, 1) #output layer: 12-dimensional input and 1-dimensional output
nn.init.constant_(self.linear_layer_4.bias, initGuess) #initial guess is put in the last layer
self.activation = nn.Tanh() #activation function
def forward(self, x): #this method defines the structure of neural network
x = self.activation(self.linear_layer_1(x)) #first hidden layer
x = self.activation(self.linear_layer_2(x)) #second hidden layer
x = self.activation(self.linear_layer_3(x)) #third hidden layer
x = self.linear_layer_4(x) #output layer
return x
def PDE_error(network, input): #error function
#dV/dk
input.requires_grad_()
V_prime = grad(outputs = network(input), inputs = input, grad_outputs=torch.ones_like(input))[0]
V_prime = torch.clamp(V_prime, min= 1E-7) #if less than 1E-7 substitute with 1E-7
Y = A * (input**alpha)
C = V_prime**(-1/gamma)
U = C**(1-gamma)/(1-gamma)
mu_K = Y - C - delta*input
PDE = U + V_prime*mu_K - rho*network(input) # PDE error
return (PDE**2).mean() #mean squared PDE error
def train_model(network, epochs): #function to train the model
losses = np.zeros(epochs) #storing losses in an array
optimizer = torch.optim.Adam(network.parameters()) # Adam is the optimizer
for epoch in range(epochs):
print(epoch) if epoch%1000 == 0 else 0
input = torch.normal(k_ss, 1, size=(batchSize, 1)) #sample from normal distribution around the steady state
input = torch.clamp(input, min=kMin, max=kMax)
optimizer.zero_grad() #zero out gradients before new update
loss = PDE_error(network, input) #calculating PDE error
loss.backward() #backpropagation
optimizer.step() #network update
losses[epoch] = loss.item() #saving the loss
return losses
# Solving the model
Value_net = neural_net(initGuess = VFInitGuess) #network is initialized
losses = train_model(Value_net, number_epochs) #training
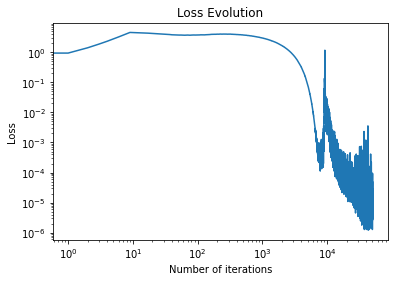
# Loss evolution
fig = plt.figure()
plt.plot(np.convolve(losses, np.ones(10)/10)) #losses are smoothed by running average
plt.xscale('log')
plt.yscale('log')
plt.xlabel('Number of iterations')
plt.ylabel('Loss')
plt.title('Loss Evolution')
plt.show()
fig.savefig('Loss_Evolution.png')
# Value and policy functions
def optimal_C(network, input): #optimal policy rule
#dV/dk
input.requires_grad_()
V_prime = grad(outputs = network(input), inputs = input, grad_outputs=torch.ones_like(input))[0]
V_prime = torch.clamp(V_prime, min= 1E-7) #if less than 1E-7 substitute with 1E-7
return V_prime**(-1/gamma)
K = np.linspace(kMin, kMax, gridSize) #define plotting grid
V = Value_net(torch.tensor(K).float().view(-1,1)).detach().numpy() #value function
C = optimal_C(Value_net, torch.tensor(K).float().view(-1,1)).detach().numpy() #optimal policy
fig = plt.figure()
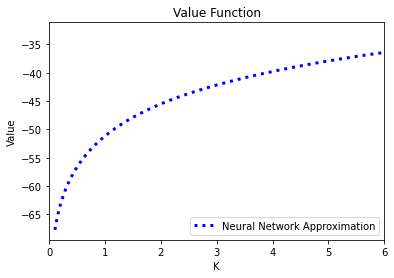
plt.plot(K, V, color = "blue", label = "Neural Network Approximation", linewidth = 3, linestyle = ':')
# plt.plot(K, reference_V, color= "orange", label = "Finite Difference Scheme", linewidth = 3, linestyle = '-')
plt.xlabel('K')
plt.ylabel('Value')
plt.title('Value Function')
plt.legend(loc = "lower right")
plt.xlim(0,6)
plt.show()
fig.savefig('Value_Function.png')
# Policy function
fig = plt.figure()
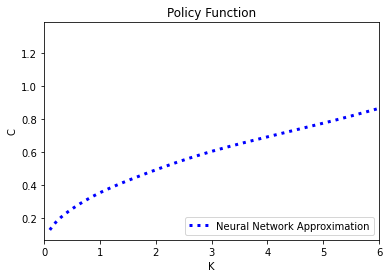
plt.plot(K, C, color = "blue", label = "Neural Network Approximation", linewidth = 3, linestyle = ':')
# plt.plot(K, reference_C, color= "orange", label = "Finite Difference Scheme", linewidth = 3, linestyle = '-')
plt.xlabel('K')
plt.ylabel('C')
plt.title('Policy Function')
plt.legend(loc = "lower right")
plt.xlim(0,6)
plt.show()
fig.savefig('Policy_Function.png')