Hi all,
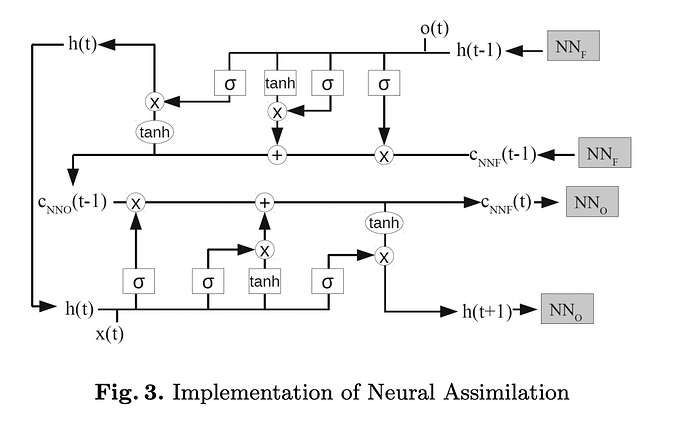
I am attempting to reproduce the Neural Assimilation model architecture described in this paper: Neural Assimilation - PMC. They are essentially trying to design an architecture that would be much faster than using a Kalman Filter by bypassing the correction step. Despite the authors providing some code in Keras, I have had some issues trying to implement this with PyTorch as I simply cannot see how they have built the model. (link to the code is here: FINAL CODE - Google Drive)
From my understanding, we need two LSTMs with one using the model forecasted data and the other using the observational data. The tricky part is that each LSTM requires as input the hidden state and cell state from the other LSTM which I am having some difficulty trying to implement. Anyone have any ideas on how I could do this? So far I have only used simple LSTMs for many-to-many prediction.
This is a diagram of the architecture:
and what I am working on thus far as its implementation:
class Neural_Assimilation(nn.Module):
def __init__(self, n_inputs, n_hidden, num_layers, n_outputs):
super(Neural_Assimilation, self).__init__()
self.D = n_inputs
self.M = n_hidden
self.K = n_outputs
self.L = num_layers
self.rnn_f = nn.LSTM(
input_size=self.D,
hidden_size=self.M,
num_layers=self.L,
batch_first=True)
self.rnn_o = nn.LSTM(
input_size=self.D,
hidden_size=self.M,
num_layers=self.L,
batch_first=True)
self.fc = nn.Linear(self.M, self.K) # For BiDir LSTM need to multiply self.M x 2
def forward(self, X_f, X_o):
# initial hidden states
h0_f = torch.zeros(self.L, X_f.size(0), self.M).to(device) # For BiDir LSTM need to multiply self.L x 2
c0_f = torch.zeros(self.L, X_f.size(0), self.M).to(device) # For BiDir LSTM need to multiply self.L x 2
# get RNN unit output
out_f, (h_t_f, c_t_f) = self.rnn_f(X_f, (h0_f, c0_f))
out_o, (h_t_o, c_t_o) = self.rnn_o(X_o, (h_t_f, c_t_f))
out_f, (h_t_o, c_t_o) = self.rnn_f(X_f, (h_t_o, c_t_o))
# we want h(t) and c(t) at the final time step so we can feed this into the other RNN
out_f = self.fc(out_f[:, -1, :])
hidden_state = h_t[:, -1, :]
hidden_out = self.fc(hidden_state)
cell_state = c_t[:, -1, :]
cell_out = self.fc(cell_state)
return out, hidden_state, cell_out
Would really appreciate your expertise!