Hello, I am a beginner PyTorch user and have been following some tutorials to learn how to build some very basic PyTorch models. After building a model to fit a linear distribution (01. PyTorch Workflow Fundamentals - Zero to Mastery Learn PyTorch for Deep Learning) I tried to create a model to fit a polynomial distribution.
The code below walks through the data generation, model construction, and training results:
import torch
import numpy as np
from torch import nn
import matplotlib.pyplot as plt
print(f'using version {torch.__version__}')
# create some known parameters
p1 = 2
p2 = -13
p3 = 26
p4 = -7
p5 = -28
p6 = 20
p7 = 1
# generate some data
def poly(x):
return p1*x**6 + p2*x**5 + p3*x**4 + p4*x**3 + p5*x**2 + p6*x + p7
size = 100
start = -1
end = 3
X = torch.arange(start, end, (end-start)/size)
y = poly(X) # + torch.normal(0, 0.75, size=(size,)) # if you want to add noise
# Train test split
X_train = torch.cat((X[:40], X[50:]))
y_train = torch.cat((y[:40], y[50:]))
X_test = X[40:50]
y_test = y[40:50]
# Build the model:
class PolynomialRegressionModel(nn.Module):
def __init__(self):
super().__init__()
self.p1 = nn.Parameter(torch.rand( 1,
requires_grad=True,
dtype=torch.float32))
self.p2 = nn.Parameter(torch.rand( 1,
requires_grad=True,
dtype=torch.float32))
self.p3 = nn.Parameter(torch.rand( 1,
requires_grad=True,
dtype=torch.float32))
self.p4 = nn.Parameter(torch.rand( 1,
requires_grad=True,
dtype=torch.float32))
self.p5 = nn.Parameter(torch.rand( 1,
requires_grad=True,
dtype=torch.float32))
self.p6 = nn.Parameter(torch.rand( 1,
requires_grad=True,
dtype=torch.float32))
self.p7 = nn.Parameter(torch.rand( 1,
requires_grad=True,
dtype=torch.float32))
def forward(self, x):
return self.p1*x**6 + self.p2*x**5 + self.p3*x**4 + self.p4*x**3 + self.p5*x**2 + self.p7*x + self.p7
# Create the model
torch.manual_seed(42)
model = PolynomialRegressionModel()
# Define the loss function and the optimizer
loss_fn = nn.L1Loss()
learning_rate = 0.0001
optimizer = torch.optim.SGD(params = model.parameters(),
lr = learning_rate)
# Train the model
epochs = 10000
epoch_num = []
train_losses = []
test_losses = []
for epoch in range(epochs):
model.train()
y_pred = model(X_train)
loss = loss_fn(y_pred, y_train)
optimizer.zero_grad()
loss.backward()
optimizer.step()
model.eval()
with torch.inference_mode():
test_pred = model(X_test)
test_loss = loss_fn(test_pred, y_test)
if epoch % 10 == 0:
epoch_num.append(epoch)
train_losses.append(loss.item())
test_losses.append(test_loss.item())
print(f'Epoch: {epoch} | MAE train loss: {round(loss.item(), 6)} | MAE test loss: {round(test_loss.item(), 6)}')
using version 1.12.1
Epoch: 0 | MAE train loss: 115.959633 | MAE test loss: 1.532966
Epoch: 10 | MAE train loss: 107.854439 | MAE test loss: 1.515569
Epoch: 20 | MAE train loss: 99.749237 | MAE test loss: 1.503134
Epoch: 30 | MAE train loss: 91.644035 | MAE test loss: 1.497113
…
Epoch: 3620 | MAE train loss: 3.567217 | MAE test loss: 2.296267
Epoch: 3630 | MAE train loss: 3.564242 | MAE test loss: 2.295868
Epoch: 3640 | MAE train loss: 3.565017 | MAE test loss: 2.296033
Epoch: 3650 | MAE train loss: 3.566075 | MAE test loss: 2.295634
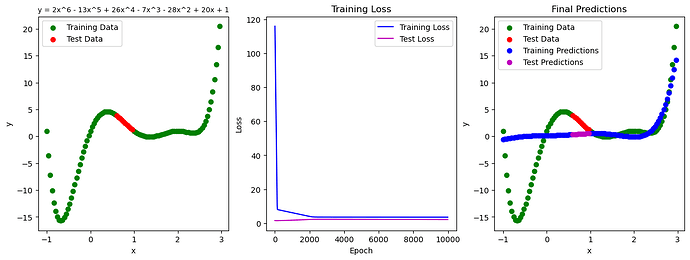
Plot the data:
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(15, 5))
# Plot the ground truth
ax1.scatter(X_train, y_train, c='g', label='Training Data')
ax1.scatter(X_test, y_test, c='r', label='Test Data')
ax1.set_xlabel('x')
ax1.set_ylabel('y')
ax1.set_title('y = 2x^6 - 13x^5 + 26x^4 - 7x^3 - 28x^2 + 20x + 1')
ax1.title.set_fontsize(9)
ax1.legend(loc='upper left')
# Plot the training loss
ax2.plot(epoch_num, train_losses, c='b', label='Training Loss')
ax2.plot(epoch_num, test_losses, c='m', label='Test Loss')
ax2.set_xlabel('Epoch')
ax2.set_ylabel('Loss')
ax2.set_title('Training Loss')
ax2.legend(loc='upper right')
# plot the final predictions
ax3.scatter(X_train, y_train, c='g', label='Training Data')
ax3.scatter(X_test, y_test, c='r', label='Test Data')
ax3.scatter(X_train, model(X_train).detach().numpy(), c='b', label='Training Predictions')
ax3.scatter(X_test, model(X_test).detach().numpy(), c='m', label='Test Predictions')
ax3.set_xlabel('x')
ax3.set_ylabel('y')
ax3.set_title('Final Predictions')
ax3.legend(loc='upper left')
As you can see, the model does a poor job fitting either the training or the test data. I have played around with MSE instead of L1 loss, as well as Adam vs SGD, but no major improvements. I think I’m missing something fundamental in either the model construction or the training loop but I’m not sure what it is.
NOTE: I am sure that there is a fancier built-in approach for fitting this type of distribution. I would be interested in hearing other approaches, but here I am specifically trying to conceptualize what is wrong with this implementation. Any feedback would be greatly appreciated.