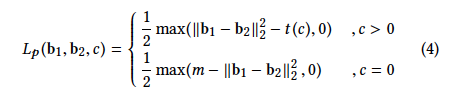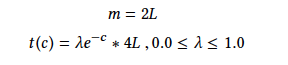Custom Loss Function Does not converge

[Mr.Bank]

Hi,
I am new in Pytorch and try to implement a custom loss function which is mentioned in a paper, Deep Multi-Similarity Hashing for Multi-label Image Retrieval.
However, the loss value from the loss function does not converge to smaller values whether used big epoch numbers or not. It plays around the started value.
I checked weight values and they are changing so I think backward mechanisms work.
So where is the problem?

The loss function:

class pairWiseLoss(nn.Module):    
    def forward(self, binaryCodes, labels):

        lambdaValue = 0.62
        
        numSample = len(binaryCodes)
        halfNumSample = numSample // 2
    
        
        similarity = torch.diagonal(torch.mm(labels[:halfNumSample], labels[halfNumSample:].t()))
        maskCommonLabel = similarity.gt(0.0)
        maskNoCommonLabel = similarity.eq(0.0)
        
        tc = torch.exp(-similarity) * lambdaValue * 4 * args.bits
        m = 2 * args.bits
        hammingDistance = torch.diagonal( torch.cdist(binaryCodes[:halfNumSample],binaryCodes[halfNumSample:], p = 0) )
        zeros = torch.zeros_like(hammingDistance)
        
        loss = torch.sum(torch.masked_select(0.5 * torch.max(hammingDistance - tc , zeros ),maskCommonLabel  )  ) +  torch.sum(torch.masked_select(0.5 * torch.max( m - hammingDistance, zeros), maskNoCommonLabel ) )
        
        return loss   

The training block:

def train(trainloader, model, optimizer, epoch, use_cuda, train_writer,gpuDisabled,customLoss):

    label_train = []
    name_train = []
    generated_codes = []
    
    
    lossTracker = MetricTracker()
    
    model.train()
    
    for idx, data in enumerate(tqdm(trainloader, desc="training")):
        
        numSample = data["bands10"].size(0)

        if gpuDisabled :
            bands = torch.cat((data["bands10"], data["bands20"],data["bands60"]), dim=1).to(torch.device("cpu"))
            labels = data["label"].to(torch.device("cpu")) 
        else:            
            bands = torch.cat((data["bands10"], data["bands20"],data["bands60"]), dim=1).to(torch.device("cuda"))
            labels = data["label"].to(torch.device("cuda"))
        

        optimizer.zero_grad()
        logits = model(bands)        
        loss = customLoss(logits, labels)

        loss.backward()
        optimizer.step()

        lossTracker.update(loss.item(), numSample)

        generated_codes += list(logits)
        label_train += list(labels)
        name_train += list(data['patchName'])
        

    train_writer.add_scalar("loss", lossTracker.avg, epoch)

    print('Train loss: {:.6f}'.format(lossTracker.avg))
    
    #s = torch.sum(model.FC.weight.data)
    #print('FC Sum Weight data: ',s)
    
    
    
    return (generated_codes,label_train,name_train)

And the model:

class ResNet50PairWise(nn.Module):
    def __init__(self, bits = 16):
        super().__init__()

        resnet = models.resnet50(pretrained=False)

        self.conv1 = nn.Conv2d(12, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
        self.encoder = nn.Sequential(
            self.conv1,
            resnet.bn1,
            resnet.relu,
            resnet.maxpool,
            resnet.layer1,
            resnet.layer2,
            resnet.layer3,
            resnet.layer4,
            resnet.avgpool
        )
        self.FC = nn.Linear(2048, bits)


        self.apply(weights_init_kaiming)
        self.apply(fc_init_weights)

    def forward(self, x):
        x = self.encoder(x)
        x = x.view(x.size(0), -1)

        logits = self.FC(x)
        sign = torch.sign(logits)
        binary_out = torch.relu(sign)

        return binary_out   

Thanks in advance

[ptrblck]

I’m not familiar with the mentioned loss function, but if you already checked the gradients, it would at least mean that the computation graph is not detached accidentally.

You could check, if the relu activation is needed at the model output, as this seems to be unusual (of course it might still fit your use case).

[Mr.Bank]

@ptrblck thanks for your message.

These are details about that loss function.
c: number of common labels between binary pairs
l: hash length

I use ReLu in the model because I want to produce only 0 and 1 from the network. That’s a hashing model so it should produce only binary results. That’s why sign and Relu have been used. Is it not an acceptable way?

Max function in loss function can not be differentiated in some cases as mentioned in

Use max operation in loss function

hi, im very confused. from all i know, mathematicly, max operation is not differential i read here a lot of contrasting answers - some people are saying that it is not differential, and therefor cant be used in a loss function and some are saying that it is differential “enough” for backpropagation does someone have an answer and a good explanation about that issue?

That’s why I changed the max function with ReLu in loss function but it still causes the same problem.

I added these two lines to existed approach to see weight updates

        loss.backward()
        optimizer.step()
        
        s = torch.sum(model.FC.weight.data)
        print(s)

And it returns:
Epoch 0:
tensor(8.6537, device=‘cuda:0’)
tensor(8.6536, device=‘cuda:0’)
tensor(8.6535, device=‘cuda:0’)

Epoch 1:
Tensor(8.6534, device=‘cuda:0’)
tensor(8.6532, device=‘cuda:0’)
tensor(8.6531, device=‘cuda:0’)

Epoch 2:
tensor(8.6529, device=‘cuda:0’)
tensor(8.6527, device=‘cuda:0’)
tensor(8.6525, device=‘cuda:0’)

Does it mean loss function update weights correctly? But loss value is still not decreasing.

[ptrblck]

The sign method would return a zero gradient wouldn’t it?
The only change in the output of sign would be at x=0, so that you might be killing the gradient with this method.

Are you sure the paper uses a sign method for its implementation?

Note that I’m just pointing to “unusual” model design choices, but it might be perfectly valid for your use case.

[Mr.Bank]

@ptrblck thanks for your pointing out. Sign method is a zero gradient so it breaks the gradients.
How can I produce only 1s and 0s from the network without that approach?

[ptrblck]

torch.sign isn’t technically breaking the computation graph, but will return a zero gradient.
I think you could use a sigmoid as a smooth approximation for values in [0, 1].
tanh would approximate the sign method or alternatively you could also use
x / (torch.sqrt(x*x + delta)).

[Mr.Bank]

They will produce value in the range not only 0s and 1s. Is there any way to create only 0s and 1s?
In the last function, you mentioned, how delta is calculated?

[ptrblck]

You could chose delta manually. The smaller it is, the more you would approximate the step function.

@Mr.Bank

Is there any way to create only 0s and 1s?

Yes, with a threshold (step function), but then you would get zero gradients, as the derivative of the step function would be the delta function, which has only a valid value at x=0 (if the step is there and not shifted).