I’m trying to input images of objects that are rotated in the xy plane and use a CNN to learn the angle of rotation in the range 0-360 degrees.
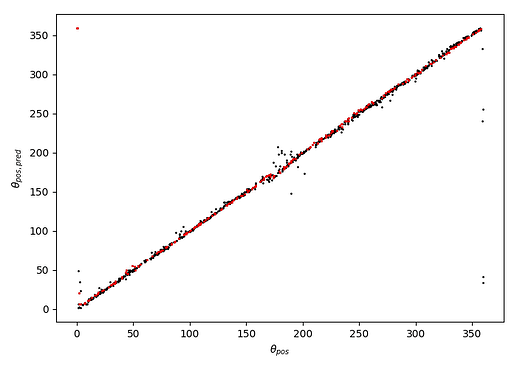
However as mentioned in many posts (eg. Data_Science) , there’s a discontinuity between 0 degrees and 360 degrees where predictions of 359.9 degrees will be penalised heavily when the true value is in fact 0 degrees and so the prediction is very close to the target but the discontinuous nature of the numerical range makes the error huge.
This results in striping at 0 and 360 degrees (and also 180 degrees) - see image below:
I want to write a custom loss function that instead looks to minimise the smallest angle between predicted and true rotation angle given that there are 4 ways in which you can measure the angle between them.
Taking the absolute of these (or the squared angular difference) makes two of these angular measurements equivalent and therefore you only have 2 ways to measure the angular difference between true and predicted angle.
Therefore my custom loss function looks as follows:
def pos_loss(output, target):
""" LOSS FUNCTION FOR POSITION ANGLE BASED ON MINIMUM ARC SEPARATION """
loss = torch.mean(torch.stack([ (output-target)**2,
(1-torch.abs(output-target))**2] ).min(dim=0)[0])
return loss
Note: the 1 in 1-torch.abs(ou... comes from my target being in the range 0-1 as I have normalised the range 0-360 to mean that I can use a sigmoid activation for the output layer and simply get back to the true angle by multiplying up by 360, post training.
And I use the loss function during a CNN training run simply by calling:
loss = pos_loss(prediction,targets)
optim.zero_grad(); loss.backward(); optim.step()
Am I missing a huge step in implementing a custom loss function here that means the way I’m using mine means no appropriate gradients can be calculated?
Using torch.nn.MSELoss() instead trains well but gives striping, but using my custom loss function gives really unstable training that often defaults to predicting close to 0 for all input examples.
Many thanks in advance and please ask as many questions as you’d like.
Extra information:
I am using:
Python 3.6.8
PyTorch 1.0.0