Custom neural network with custom activation functions and also non-linear layers

autograd
1

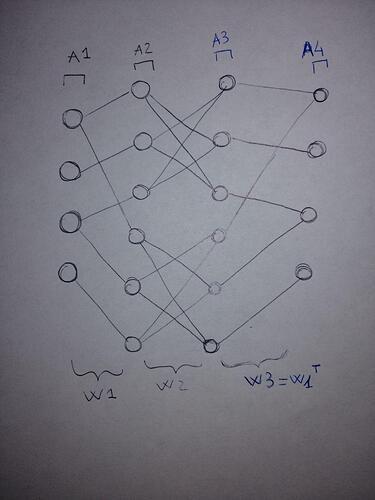
I am trying to build the so called Neural Network Decoder in pytorch to train it, but I have problems in the implementation.

NN_decoder
NN_decoder960×1280 86.8 KB

What I want to build is a neural network starting from the following numpy functions, that I wrote and checked and they are working correctly, where “received” is a vector of +1s and -1s with noise added.

“n1” and “n2” are the number of neurons in layer 1 and 2 respectively.

A1=LLR(received,variance) # LLR is just the log-likelihood ratio, A1 are the inputs of the wanted neural network
I=A1.copy() # I is my input
for i in range(repeated_times):
    s_estimated=1-(A1>0) # estimated string of bits
    if np.sum(np.remainder(np.matmul(s_estimated,H),2))==0: # check if the estimated string is a codeword, in case exit
        break
        
    A2=np.tanh(np.matmul(W1.T,A1.T)/2) # first hidden layer where W1 is matrix containing the weights that connect A1 to A2, and are the parameters that I want to train
    M1=np.multiply(W2,np.repeat(A2,n2,1)) # M1 and A3 are 1 operation, cause A3 is not a linear layer, but it performs the multiplication of its inputs. W2 are fixed weights for the entire process
    A3=2*np.arctanh(np.prod(M1+(M1==0),axis=0))
    A4=I+np.matmul(A3,W1.T) # A4 is the last layer, an usual linear layer. W1 is the same weight matrix used at A2. So I want to do a weight-sharing between layers
    A1=A4 # the network is repeated a certain number of times

What I did to convert it in “torch language” was the following:

def SPA_tanh(W,A):
    W1=W.detach().numpy()
    A1=A.detach().numpy()
    return torch.from_numpy(np.tanh(np.matmul(W1.T,A1.T)/2))
    
def SPA_arctanh(W, A, n2):
    W2=W.detach().numpy()
    A2=A.detach().numpy().T
    M1=np.multiply(W2,np.multiply(A2,np.ones((n2,n2)))).T
    A3=2*np.arctanh(np.prod(M1+(M1==0),axis=0))
    return torch.from_numpy(A3)

def SPA_output(W, A, In):
    I=In.detach().numpy()
    W3=W.detach().numpy()
    A3=A.detach().numpy()
    return torch.from_numpy((I+np.matmul(A3,W3)))

def SPA_sigmoid(A):
    A4=A.detach().numpy()
    return torch.from_numpy(1/(1+np.exp(-A4)))

and then I used those functions as follow:

inputs=torch.from_numpy(LLR(received,sigma))
A1=torch.from_numpy(inputs.numpy().copy())
for i in range(repeated_times):
    s_estimated=1-(A1.numpy()>0)
    if np.sum(np.remainder(np.matmul(s_estimated,H),2))==0:
        break
    A2=SPA_tanh(torch.from_numpy(W1),A1)
    A3=SPA_arctanh(torch.from_numpy(W2),A2,n2)
    A4=SPA_output(torch.from_numpy(W1.T),A3,inputs)
    A1=torch.from_numpy(A4.numpy().copy())

Outputs_estimated=SPA_sigmoid(A4).numpy()
loss=(1/(2*outputs.size)*np.sum(np.power((1-Outputs_estimated)-Y_true,2))) # generic loss, just to understand if it works

First problem in this way I will not obtain a neural network, and unluckily I am aware of this. I tried to implement the functions as layers of a neural network but every time there are errors. Here an example of one of the functions implemented:

class SPA_tanh(nn.Module):
    def __init__(self):
        super(SPA_tanh, self).__init__()

    def forward(self, input):
        A1=input.detach().numpy()
        W1=self.weight.detach().numpy()
        print(W1)
        output = torch.from_numpy(np.tanh(np.matmul(W1.T,A1.T)/2))
        return output

Can anyone help me in understanding what is wrong?
Moreover, how can I pass to the class also the precomputed weight matrices W1 as initialization of the self.weights? (or W2 for the other functions)

How can I be sure that only some weights will be trained by the network (W1) and others no (W2)? And how can I share the weights?

I apologize for my ignorance.

2

As a first pass response you can use the Module class for your 1st and 3rd layers. As I understand these layers use the same weight matrix but transposed. This is an interesting implementation, but to ensure that the parameter updates are correct, you should actually have one self.weight matrix that is applied twice within the module, either in the original or transponsed form. You would still need two bias vectors

So the forward pass would be like:

def forward (input, first=False):
    if first:
        out = torch.matmul(input, self.w) + self.b_1
    else:
        out = torch.matmul(input, self.w.T) + self.b_2

Where self.w is a parameter layer of shape (n1, n2) and self.b_1 has shape (n1) and self.b_2 has shape (n2).