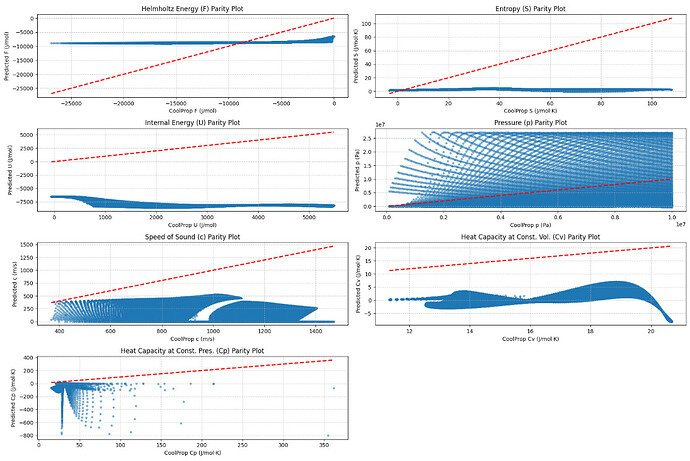
Hi all,
I’m training a physics-informed neural network (PINN) in PyTorch to predict the molar Helmholtz free energy and related thermodynamic properties (S, U, P, c, Cv, Cp) for hydrogen, using a custom loss function that combines data fidelity and physics constraints via automatic differentiation. However, my loss function is not converging and the parity plots show no meaningful trends after training. My input variables are T and rho and predicting F subjected to physics constraints from (S,U,P,Cv,Cp and c). All properties are scaled using Z-score
my custom loss function:
— Custom Loss Function with Physics Constraints —
def custom_loss(outputs_F_scaled, targets_F_scaled, inputs_X,
targets_S_scaled, targets_U_scaled, targets_P_scaled, targets_c_scaled,
targets_Cv_scaled, targets_Cp_scaled, # New: Cv and Cp targets
rho_mean, rho_std, T_mean, T_std, F_std, S_mean, S_std, U_mean, U_std, P_mean, P_std, c_mean, c_std, Cv_mean, Cv_std, Cp_mean, Cp_std, M_molar): # New: Cv and Cp scaling params
“”"
Calculates the total loss, combining data fidelity (MSE for F) and
physics-informed constraints (MSE for S, U, P, c, Cv, and Cp).
“”"
# Data fidelity loss: Mean Squared Error between predicted and true scaled F
mse_F_loss = nn.MSELoss()(outputs_F_scaled, targets_F_scaled)
# Calculate first-order derivatives of F_scaled with respect to rho_scaled and T_scaled
grad_output = torch.autograd.grad(outputs=outputs_F_scaled.sum(), inputs=inputs_X,
create_graph=True, retain_graph=True)[0]
dF_drho_scaled = grad_output[:, 0].reshape(-1, 1) # d(F_scaled)/d(rho_scaled)
dF_dT_scaled = grad_output[:, 1].reshape(-1, 1) # d(F_scaled)/d(T_scaled)
# Calculate second-order derivatives of F_scaled
d2F_drho2_scaled = torch.autograd.grad(outputs=dF_drho_scaled.sum(), inputs=inputs_X,
create_graph=True, retain_graph=True)[0][:, 0].reshape(-1, 1)
d2F_dT2_scaled = torch.autograd.grad(outputs=dF_dT_scaled.sum(), inputs=inputs_X,
create_graph=True, retain_graph=True)[0][:, 1].reshape(-1, 1)
d2F_drho_dT_scaled = torch.autograd.grad(outputs=dF_drho_scaled.sum(), inputs=inputs_X,
create_graph=True, retain_graph=True)[0][:, 1].reshape(-1, 1)
# Unscale inputs for use in physical relations
T_unscaled = inputs_X[:, 1].reshape(-1, 1) * T_std + T_mean
rho_unscaled = inputs_X[:, 0].reshape(-1, 1) * rho_std + rho_mean
# Calculate unscaled first-order derivatives needed for S, U, P
dF_dT_unscaled = dF_dT_scaled * (F_std / T_std)
dF_drho_unscaled = dF_drho_scaled * (F_std / rho_std)
# Calculate unscaled second-order derivatives needed for speed of sound, Cv, Cp
d2F_drho2_unscaled = d2F_drho2_scaled * (F_std / rho_std**2)
d2F_dT2_unscaled = d2F_dT2_scaled * (F_std / T_std**2)
d2F_drho_dT_unscaled = d2F_drho_dT_scaled * (F_std / (rho_std * T_std))
# Predicted unscaled S, U, P based on fundamental thermodynamic relations
S_pred_unscaled = -dF_dT_unscaled
U_pred_unscaled = (outputs_F_scaled * F_std + F_mean) + T_unscaled * S_pred_unscaled
p_pred_unscaled = rho_unscaled**2 * dF_drho_unscaled
# Predicted speed of sound squared (c^2) using molar Helmholtz energy relation
epsilon = 1e-9
denominator_for_c2 = d2F_dT2_unscaled
denominator_for_c2 = torch.clamp(denominator_for_c2, min=epsilon)
c_squared_pred_unscaled = (1 / M_molar) * (
rho_unscaled**2 * d2F_drho2_unscaled -
(d2F_drho_dT_unscaled**2) / denominator_for_c2
)
# Ensure c_squared is non-negative before taking the square root
c_squared_pred_unscaled = torch.relu(c_squared_pred_unscaled)
c_pred_unscaled = torch.sqrt(c_squared_pred_unscaled)
# New: Predicted Cv and Cp based on fundamental thermodynamic relations
# Cv = -T * (d2F_m/dT^2)_rho_m
Cv_pred_unscaled = -T_unscaled * d2F_dT2_unscaled
# Cp = Cv - T * (d2F_m/(drho_m dT))^2 / (d2F_m/drho_m^2)_T
denominator_for_Cp = d2F_drho2_unscaled
denominator_for_Cp = torch.clamp(denominator_for_Cp, min=epsilon) # Ensure non-zero denominator
Cp_pred_unscaled = Cv_pred_unscaled - T_unscaled * (d2F_drho_dT_unscaled**2) / denominator_for_Cp
# Scale predicted S, U, P, c, Cv, Cp for comparison with scaled true values in the loss function
S_pred_scaled = (S_pred_unscaled - S_mean) / S_std
U_pred_scaled = (U_pred_unscaled - U_mean) / U_std
P_pred_scaled = (p_pred_unscaled - P_mean) / P_std
c_pred_scaled = (c_pred_unscaled - c_mean) / c_std
Cv_pred_scaled = (Cv_pred_unscaled - Cv_mean) / Cv_std
Cp_pred_scaled = (Cp_pred_unscaled - Cp_mean) / Cp_std
# Physics-informed loss components (MSE for S, U, P, c, Cv, Cp)
mse_S_loss = nn.MSELoss()(S_pred_scaled, targets_S_scaled)
mse_U_loss = nn.MSELoss()(U_pred_scaled, targets_U_scaled)
mse_P_loss = nn.MSELoss()(P_pred_scaled, targets_P_scaled)
mse_c_loss = nn.MSELoss()(c_pred_scaled, targets_c_scaled)
mse_Cv_loss = nn.MSELoss()(Cv_pred_scaled, targets_Cv_scaled)
mse_Cp_loss = nn.MSELoss()(Cp_pred_scaled, targets_Cp_scaled)
# --- Adjusted Physics Loss Weights (Revised for better balance) ---
total_physics_loss = (0.5 * mse_S_loss +
0.5 * mse_U_loss +
0.5 * mse_P_loss +
0.8 * mse_c_loss +
0.5 * mse_Cv_loss +
0.5 * mse_Cp_loss)
# Weight for the physics-informed loss (overall physics loss)
physics_loss_weight = 0.01
total_loss = mse_F_loss + physics_loss_weight * total_physics_loss
return total_loss, mse_F_loss, mse_S_loss, mse_U_loss, mse_P_loss, mse_c_loss, mse_Cv_loss, mse_Cp_loss # New: return Cv, Cp losses
- Why is my loss not converging and predictions so far off?
- Are there common pitfalls with autograd-based physics constraints or scaling?
- Any suggestions to debug or improve the custom loss function?
I have a model working really well with F and when taking derivatives getting very close values for S,U and P but problematic when adding Cv ,Cp and speed of sound physics( second order partial derivatives).
Thanks for any help!