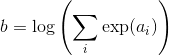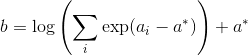Dealing with NaN's in gradients

1

I am trying to train a Mixture Density Network, by reproducing the results of the toy example of section 5 of Bishop’s paper, where MDNs were initially proposed (link to the paper: https://publications.aston.ac.uk/373/1/NCRG_94_004.pdf).

I am using exactly the same network architecture proposed there (single hidden layer with 20 neurons and tanh activation). The only difference is that I am using SGD instead of BFGS as my optimization algorithm.

Unfortunately, after 2k or 3k iterations (where the loss reduces considerably), I start getting NaN’s as the loss value. After some intense debug, I finally found out where these NaN’s initially appear: they appear due to a 0/0 in the computation of the gradient of the loss w.r.t. the means of the gaussian.

I am using negative log-likelihood as the loss function, L=-sum(log(p_i)). Therefore, the gradient of L w.r.t. p_i is

dLdp= -1/p_i

However, the derivative of a Gaussian function w.r.t. its mean, mu, is:

dpdmu = p_i * (x_i-mu_i)/(sigma_i^2)

so it is proportional to p_i. Therefore, when p_i is close to 0, the derivative of the loss w.r.t. the mean is:

dLdmu = dLdp * dpdmu = 0/0 -> NaN

However, this indetermination is easy to eliminate, since the expression may be algebraically simplified to dLdmu = (mu_i - x_i)/sigma_i^2. Of course, all that PyTorch does is numeric computing, so it is not able to do this simplification. How can I deal with this issue? Can I at least replace NaN’s with something else (zeros, for instance), so that they do not propagate?

(In all my reasoning I have assumed a MDN with one single Gaussian kernel, which is kind of stupid, but similar results roughly apply if we consider multiple kernels.)

Thank you in advance.

2

Hello @dpernes

I think it is most common to give the expression for the log likelihood in “one go” in that you do not compute dLdp.
The weights of your components will sum to one, so you can compute the per-component log likelihoods and then do the usual log-sum-exp stabilisation to safely get from per-component log likelihood to the full one.

Best regards

Thomas

1 Like
3

Hi @tom. Thank you for your reply!

Do you mean that I should write the expression for the log of p directly, instead of computing p and then applying log() to p? That seems a good idea, I will check if that works.

EDIT: After thinking a bit, that does not seem to be useful when I have more than one Gaussian component. Suppose that my Gaussian mixture has two components. Then, p is given by:

p = a0exp(b0(x-u0)^2) + a1exp(b1(x-u1)^2)

where a0, b0, a1 and b1 are some constants and u0 and u1 are the means. If we apply log() to p, there is no obvious way to simplify the expression, since we get the logarithm of a sum…

4

Hello,

That is the log-sum-exp computation I mentioned.
I have implemented something that sounds similar to what your description in the GaussianMixture1d’s forward method in this
1d Mixture Density Network notebook.

Best regards

Thomas

1 Like
5

Got it, thank you!! :slight_smile:

6

Hi. I met the same problem as you. Could you please show me your modified code about loss computation?Thanks!

7

Hi Jethro,

Unfortunately, I can’t find the source code (this was for a toy example that I might have deleted).
However, scipy has an (open source) implementation of the log-sum-exp operation (see below), which is easy to adapt for PyTorch.

Moreover, the idea behind this function is very simple, so if you understand it you might not even need to look at the scipy code. Let me explain.

Log-sum-exp, like its name says, computes the logarithm of a sum of exponentials:

image

If the values inside the exponentials are all large negative numbers, the sum inside the log vanishes and we get the logarithm of 0, so we’re in trouble. To avoid this, the following simple trick is used:

  1. Find the maximum value among the a_i’s:
    image

  2. Compute b using:
    image

Now, at least one of the values inside the exponentials will be 0, and exp(0) = 1, so we will certainly not get log(0). Thus, we now have a numerically robust implementation of the log-sum-exp operation.

Hope this explanation helps :slight_smile:

8

Thank you very much, your answer has given me a lot of help.

1 Like
9

UPDATE: At least from version 0.4.1, PyTorch has a built-in log-sum-exp function. See link below.

https://pytorch.org/docs/stable/torch.html#torch.logsumexp

10

I am still getting nans for some reason, trying to train mixture of gaussians

11

Like @dpernes , the issue is with the sum of exponentials, in my case wrt the categorical variable. Applying his trick works. Also, see “get_mixture_coef” here: Mixture Density Networks with TensorFlow | 大トロ

12

Still not fixed actually. Check this repo, the categorical logits are nan’ing out:

Okay, I fixed it by applying a tanh before the final linear layer. No more nans, the tanh chokes the magnitude of the final layer…