I am doing an optimization problem.
Background:
Agents talk with each other in a graph. The initial states of each agent can be described as distributions x. Then they will maximize their (intimacy - privacy loss) with adding noise u.
Let’s say we have 3 nodes or 3 agents. Each of them is trying to maximize their objective funtion obj_1, obj_2 and obj_3 respectively.
The way they do the optimization is to find a u (adding noise) for themselves.
Previously, what I did is as follows. That means I am trying to find a u to max the mean of (obj_1 + obj_2 + obj_3). That works.
(the shape of u: (80, 3, 50). 80 means they talk with each other 80 times, 3 means 3 nodes, 50 means how many bins in the initial information distribution)
net.u.requires_grad = True
optimizer = torch.optim.Adam([net.u], lr=1e-3)
optimizer.zero_grad()
for i in range(0, iteration):
obj = - net.obj(x, T=T).mean() obj.backward() optimizer.step() optimizer.zero_grad()
However, currently, the target changes. Each of the agent should play their own strategy to optimize their objective function separately. But as before, they will still exchange information. So I have to find u for each of them one by one not together. So I wrote the code as follows to try to find an optimized u for agent 1.
u,shape = (T, node, nbins) = (80, 3, 50)
net.u.requires_grad = True
obj_0 = -net.obj(x, T = T)[0]
grad = torch.autograd.grad(obj_0, net.u)[0]
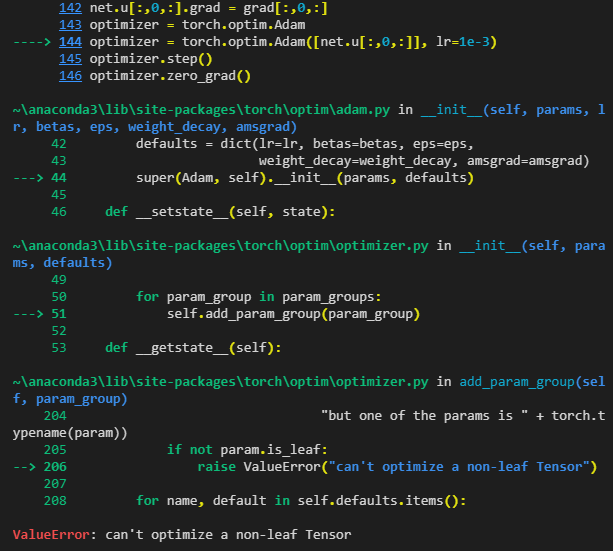
net.u[:,0,:].grad = grad[:,0,:]
optimizer = torch.optim.Adam
optimizer = torch.optim.Adam([net.u[:,0,:]], lr=1e-3)
optimizer.step()
optimizer.zero_grad()
However, there some errors as follows.
Can I ask how solve this? Or any suggestions to do such optimization with Pytorch?
Thank you so much!