Difference between 2 reshaping operations (reshape vs permute)

coyote · November 28, 2018, 8:31am

Hi everyone,

Recently, I asked this question. Though I got an answer for my original question, last comment confused me a little bit.

I don’t understand the difference between these two cases:

According to answers, this is a safe operation:

bs,seq_len,input_size= 5,20,128
x = torch.rand(bs,seq_len,input_size)
torch.reshape(x,(x.shape[0],x.shape[1],1,x.shape[2])

However, if I want to change the shape (bs, seq_len, input_size) matrix x into (seq_len, bs, input_size), it is said that I should use x.permute(1, 0, 2) rather than reshape.

Why these two cases differs from each other ?

JuanFMontesinos · November 28, 2018, 10:10am

Im not sure about reshape.
Permute is a multidimensional rotation saying somehow. It keeps the data ordering. View (which is another reshaping method) maps from one dimensionality to another sequentially reading data from the upper dimensions to the lower ones.

So if you want fuse two dimensions into one, you have to apply it over contiguous dimensions or u will modify the data ordering

coyote · November 28, 2018, 10:12am

Thanks for the reply. How do I make sure that I am doing it over contiguous dimensions or not ? Could you, if possible, give me an example on a small tenser with a contiguous and non-contiguous dimensions ?

JuanFMontesinos · November 28, 2018, 11:40am

if u have a cube

c=torch.rand(3,4,5)

and you use permute

c=torch.rand(3,4,5)
rx  = c.permute(0,2,1)
ry  = c.permute(2,1,0)
rz = c.permute(1,0,2)
print(rx.size())
print(ry.size())
print(rz.size())

torch.Size([3, 5, 4])
torch.Size([5, 4, 3])
torch.Size([4, 3, 5])

you are just rotating the tensor, but order is preserved
On the other hand, if you reshape you can see you are modifying the ordering because this is not rotating the cube but mapping in an ordered way from right to left. It takes numbers until it fills the dimensions.

sx = c.view(3,5,4)
rx - sx

That’s why this operation is different from 0

So an example about how to apply view could be the following one

if you have a tensor m= BxNxHxW
and these tensor contains B batches of N images whose size is HxW and you want to make a montage of these images in a single one concatanating in the colums your outgoing dimension would be

B,H,WxN which is equivalent to B,H,NxW

So lets see what happens if you reshape vs permute + reshape vs permute without paying attention

Im gonna mix this images

with this code

import imageio as skio
import matplotlib.pyplot as plt
import numpy as np
import torch
im1 = np.mean(skio.imread('/home/jfm/Downloads/dog.jpg'),axis=2)
im2 = np.mean(skio.imread('/home/jfm/Downloads/cat.jpg'),axis=2)[:618,:1100]

m = np.stack([im1,im2])
m = torch.from_numpy(np.stack([m,m,m]))
print(m.size())
#torch.Size([3, 2, 618, 1100])


m_reshape = m.view(3,618,1100*2).numpy()

m_permute_wrong = m.permute(0,2,3,1).contiguous().view(3,618,1100*2).numpy()
m_permute_right = m.permute(0,2,1,3).contiguous().view(3,618,1100*2).numpy()

I’m converting RGB images to gray and croping to have same size
Then creating 3 batches of 2 images

The cat cropped looks like that (that’s grayscale)

if you just reshape you get a wrong ordering

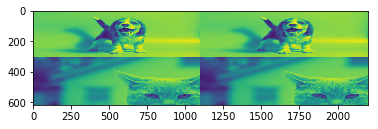
What’s going on there? as you are reordering it’s getting the information in the original order which is, all colums of image 1, all rows of image 1, all colums of image 2, all rows of image 2 and so on. If u pay attention it 's resized to be fit in the desired shape

if you permute and set dimensions before reshaping
but you do it wrongly
you get this

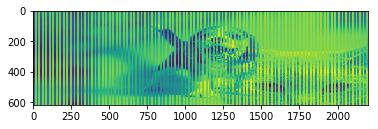
here you are filling taking the info of one image and then the other because u set N at the right. So it takes the information of the image1, colum 1, then image2, colum 1 and so on.
However if u properly order the dimensions

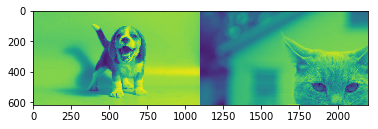
You achieve what you want which is all the colums of image 1, all the colums of image 2

Moral of this,

If you want to reshape the ordering only remains for contiguous dimensions. [1,2,3,4]
Contiguous here mens 1-2, 2-3 even 1-2-3, but not 1-3 for example.

To do so use permute and the brain first

jon · May 23, 2019, 7:00pm

Great answer and great examples! I have a question: can you explain why the m_reshape gives us the result we get? The original dimensions are

B x N x H x W

Now, when we reshape, we want something like:
B x H x W x N , so that the images are side-by-side/concatenated together along the x-axis. Here, N = 2, so we should have two images.

So why do we get 4 images with the reshape? Why don’t we get something like the top half of the dog on the left, then the bottom half of the dog on the right? Thanks!

JuanFMontesinos · May 24, 2019, 12:41am

Oh it’s actually very funny.
#torch.Size([3, 2, 618, 1100])
In this composition you have a BatchxImagesxrowsxcolums
so when you reshape it takes pixels from dimensions at the right and places them until filling new shape dimensions

so this means it goes to
m[0,0,0,0] takes that pixel and goes to m_reshape[0,0,0]
so it is filling the row 0 of m_reshape with colum pixels from m. Those pixels are dog image in fact.
The problem is that in m, in dimension 3 you have 1100 elements, meanwhile in dimension 2 of m_reshape you have 2200 elements, so it actually takes 2 rows from m to fill a row of m_reshape.

That’s why you can see that streching efect on the image. You are basically taking dogs[0::2] to create the image on the top left and then dogs[1::2] to create image in the top right.
Obviously when dog image is finished, this is, when you have already used m[0,0,:,:] it takes moves to m[0,1,:,:] to keep taking pixels. That dimension corresponds to cat and basically has same effect. The interesting point is that as you are using 2 rows of m to fill a colum of m_reshape, you are later on filling those “missing” colums with cat info creating this strange composition.

I hope you could understand my messy explanation

mkarthick271 · September 12, 2019, 1:56pm

Hi John, what is happening is that for the dog image, there are 618 rows, and to fulfill the new size of 11002 columns, the rows are alternatively placed in the same row. .For example, 1st row remains in the same place, the 2nd row is picked and placed adjacent to this 1st row. The rows of the dog image are placed alternatively in adjacent manner due to which there are 618/2 rows in the first dog image and the remaining 618/2 rows are in the 2nd dog image. so it is basically rescaled to 3142200. The same explanation goes for the cat image. Hence, the images are not cut in half horizontally but rescaled.