Difference between MeanSquaredError & Loss (where loss = mse)

[pytorchnewbie]

Hi!

So I am trying to calculate the average mean squared error over my validation dataset. I’ve done this in two ways: using Ignite’s Loss metric, where the loss_fn = nn.MSELoss() and then using Ignite’s MeanSquaredError metric, as can be seen in the code snippets below:

loss_fn = torch.nn.MSELoss()

metrics = {
        "mse": Loss(
            loss_fn,
            output_transform=lambda infer_dict: (infer_dict["y_pred"], infer_dict["y"]),
        ),
    }

    for name, metric in metrics.items():
        metric.attach(engine, name)

vs.

metrics = {
        "mse": MeanSquaredError(
            output_transform=lambda infer_dict: (infer_dict["y_pred"], infer_dict["y"]),
        ),
    }

    for name, metric in metrics.items():
        metric.attach(engine, name)

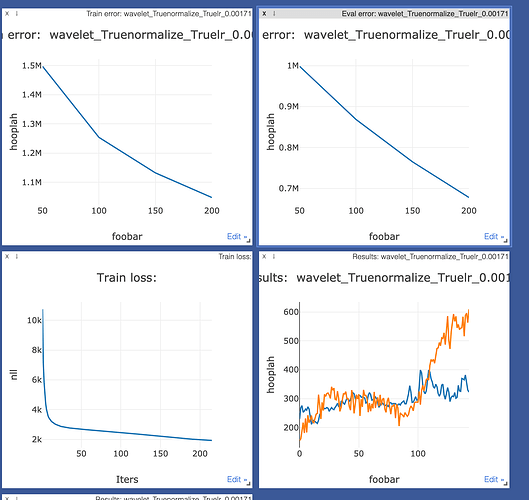
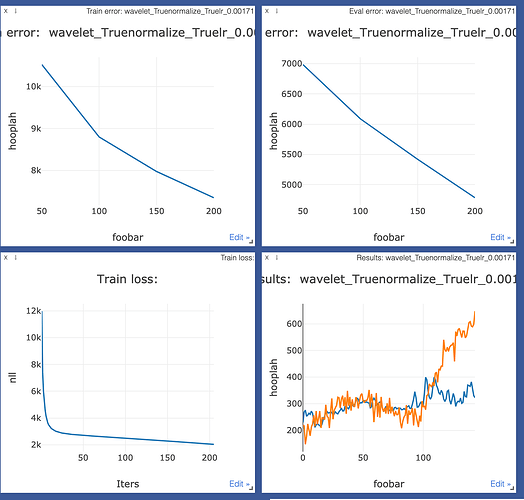
I obtain two different results, as can be sceen from the two images below.

MeanSquaredError (the top left is evaluation MSE error, and top right is training MSE error):

Loss:

We can see that MSE has an error of the order of “M” whereas Loss has an error of the order of “K”. What accounts for this difference?

Initially I thought that its probably because Loss() probably calculates the average mean squared error per batch, and then takes the average of the averages, whereas MeanSquaredError (from what I saw in the source code) keeps track of all squared errors, and takes the average of all the squared errors across all the batches (so it only does one average, not average of averages). However, since the batch size is constant, the two results should be numerically equivalent. For example:

( (((7^2) + (8^2) + (13^2))/3) + (((3^2) + (6^2) + (11^2))/3) ) / 2

is the same as:

(7^2) + (8^2) + (13^2) + (3^2) + (6^2) + (11^2)/6

because both groups in the first example have 3 elements in them.

Therefore, what accounts for the difference in magnitudes of the error functions?

Thanks so much!

[vfdev-5]

Ignite’s Metric API allows to inspect what happens batch by batch. All metrics allow to do the following:

mse_metric = MeanSquaredError()

mse_metric.reset()

mse_metric.update((y_pred1, y1))
# check result of the 1st batch
print(mse_metric.compute())

mse_metric.update((y_pred2, y2))
# check result of the 1st and 2nd batch
print(mse_metric.compute())

In this way you can compare both on your predictions and targets and see where comes from the difference.

HTH

PS.
Shouldn’t loss_fn = torch.nn.MSELoss() have reduction “sum” ?

[pytorchnewbie]

So I did that and it turns out that MeanSquaredError metric has a different output than the Loss = torch.nn.MSELoss() even on the first batch.

From running:

        loss.backward()
        optimizer.step()

        mse_metric.reset()
        loss_metric.reset()

        mse_metric.update((y_pred, y))
        loss_metric.update((y_pred, y))

        print(mse_metric.compute())
        print(loss_metric.compute())

I got :

8.566025390625
0.05948628857731819

[pytorchnewbie]

I have printed both update() steps after one iteration. They both have the same # _num_examples but loss has a different ._sum (37521646.875) than MeanSquaredErrors’ _sum_of_squared_errors (5403117056.0)… Is there a way to inspect even deeper the reason for this?

On a separate note, the _num_examples is wrong. In both cases, Loss and MeanSquaredError, te _num_examples is just the first element of the y.shape[0]. However, I want to do MSE on a tensor of [200,144], so the num_examples shouldn’t be 200, it should be 200*144. Is there a reason for why Ignite metrics only include the batch # as the num_examples?

[pytorchnewbie]

Also no it should not be “sum” because “Loss” documentation specifically says that it expects it to be the average loss. The source code then explains why it says: self._sum += average_loss.item() * n

[pytorchnewbie]

Ok i finally solved it . Loss uses torch.nn.MSELoss() which takes the sum of the errors of the (200,144) and then divides by 144, and this is then the ._sum value. The MeanSquaredError also takes the sum of the error of the (200,144), giving the _sum_of_squared_errors value. But then, during compute(), both consider the num_of_examples to be 200 so then they both divide by 200. So Loss is basically = MeanSquaredError/144. I think this is probably something alot of people could get confused about - it might be worth specifying that MeanSquaredError only divides by the batch size to get the mean…

[vfdev-5]

Thanks for pointing out this difference ! Yes, both metrics should be definitely made coherent between each other and the result of nn.MSELoss … and we also need to update the docs.

If you would like to help us by opening an issue on that, it would be great !

[pytorchnewbie]

Sure!! Ill have to learn how to do that first though haha.

Just a last thought: I do think the way MeanSquaredError does it is superior to the way Loss (well, pytorch’s torch.nn.MSELoss) does it. The assumption makes more sense. If I have a tensor of (200,144) and take the total squared error, it is more likely that the user wants the mean error w respect to the batch than w respect to the dimensions of 144…