Of course.
The code is the following:
import torch
import numpy as np
import scipy.signal as sig
import torch.nn.functional as F
import matplotlib.pyplot as plt
def numpy_periodic_conv(f, k):
H, W = f.shape
periodic_f = np.hstack([f, f])
periodic_f = np.vstack([periodic_f, periodic_f])
conv = sig.convolve2d(periodic_f, k, mode='same')
conv = conv[H // 2:-H // 2, W // 2:-W // 2]
return periodic_f, conv
def torch_periodic_conv(f, k):
H, W = f.shape[-2:]
periodic_f = f.repeat(1, 1, 2, 2)
conv = F.conv2d(periodic_f, k, padding=1)
conv = conv[:, :, H // 2:-H // 2, W // 2:-W // 2]
return periodic_f.squeeze().numpy(), conv.squeeze().numpy()
def torch_fourier_conv(f, k):
pad_x = f.shape[-2] - k.shape[-2]
pad_y = f.shape[-1] - k.shape[-1]
expanded_kernel = F.pad(k, [0, pad_x, 0, pad_y])
fft_x = torch.rfft(f, 2, onesided=False)
fft_kernel = torch.rfft(expanded_kernel, 2, onesided=False)
real = fft_x[:, :, :, :, 0] * fft_kernel[:, :, :, :, 0] - \
fft_x[:, :, :, :, 1] * fft_kernel[:, :, :, :, 1]
im = fft_x[:, :, :, :, 0] * fft_kernel[:, :, :, :, 1] + \
fft_x[:, :, :, :, 1] * fft_kernel[:, :, :, :, 0]
fft_conv = torch.stack([real, im], -1) # (a+bj)*(c+dj) = (ac-bd)+(ad+bc)j
ifft_conv = torch.irfft(fft_conv, 2, onesided=False)
return expanded_kernel.squeeze().numpy(), ifft_conv.squeeze().numpy()
if __name__ == '__main__':
f = np.concatenate([np.ones((10, 5)), np.zeros((10, 5))], 1)
k = np.array([[1, 0, -1], [2, 0, -2], [1, 0, -1]])
f_tensor = torch.from_numpy(f).unsqueeze(0).unsqueeze(0).float()
k_tensor = torch.from_numpy(k).unsqueeze(0).unsqueeze(0).float()
np_periodic_f, np_periodic_conv = numpy_periodic_conv(f, k)
tc_periodic_f, tc_periodic_conv = torch_periodic_conv(f_tensor, k_tensor)
tc_fourier_k, tc_fourier_conv = torch_fourier_conv(f_tensor, k_tensor)
print('Spatial numpy conv shape= ', np_periodic_conv.shape)
print('Spatial torch conv shape= ', tc_periodic_conv.shape)
print('Fourier torch conv shape= ', tc_fourier_conv.shape)
r_np = dict(name='numpy', im=np_periodic_f, k=k, conv=np_periodic_conv)
r_torch = dict(name='torch', im=tc_periodic_f, k=k, conv=tc_periodic_conv)
r_fourier = dict(name='fourier', im=f, k=tc_fourier_k, conv=tc_fourier_conv)
titles = ['{} im', '{} kernel', '{} conv']
results = [r_np, r_torch, r_fourier]
fig, axs = plt.subplots(3, 3)
for i, r_dict in enumerate(results):
axs[i, 0].imshow(r_dict['im'], cmap='gray')
axs[i, 0].set_title(titles[0].format(r_dict['name']))
axs[i, 1].imshow(r_dict['k'], cmap='gray')
axs[i, 1].set_title(titles[1].format(r_dict['name']))
axs[i, 2].imshow(r_dict['conv'], cmap='gray')
axs[i, 2].set_title(titles[2].format(r_dict['name']))
plt.show()
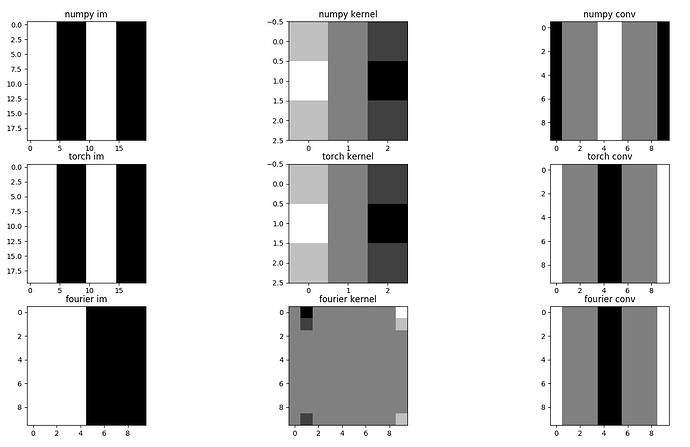
And the results are the following: