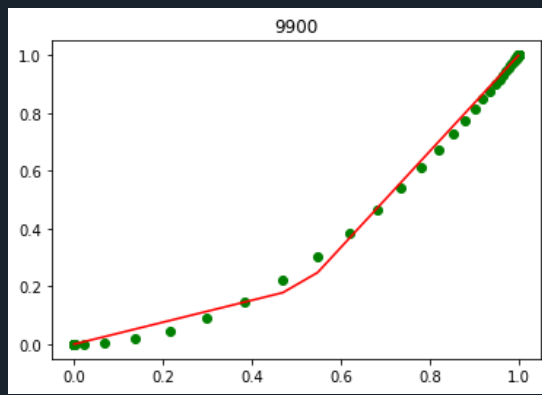
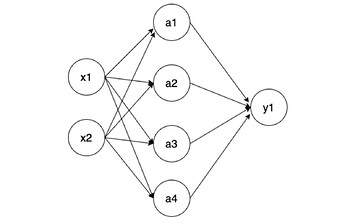
We can take a look at a little example
a = torch.rand(3, 2)
If we print a we get something like this
print(a)
# tensor([[0.9699, 0.6693],
# [0.1688, 0.0404],
# [0.7409, 0.6294]])
If we print it like this, it will just flatten the tensor into a one dimensional vector.
print(a.view(-1))
# tensor([0.9699, 0.6693, 0.1688, 0.0404, 0.7409, 0.6294])
If we now use the first of your options, we see that we gained a dimension. Now, each value is inside its own vector.
print(a.view(-1, 1))
# tensor([[0.9699],
# [0.6693],
# [0.1688],
# [0.0404],
# [0.7409],
# [0.6294]])
If we now do your second option we gain another dimension. The values are further isolated.
print(a.view(-1, 1, 1))
#tensor([[[0.9699]],
#
# [[0.6693]],
#
# [[0.1688]],
#
# [[0.0404]],
#
# [[0.7409]],
#
# [[0.6294]]])
However, the values are always the same.
You are then feeding these values to a nn.Linear layer that might look like this.
But as we mentioned, the input values remain the same. We only added more “isolation” to the values, but they are both of the size 1. So, the same inputs are going to the same network.
So, my guess for this particular case is that this should not play that much of a role. It would be more significant if you played with the input size of your linear layer (which should match the last dimension of your input).
In order to be sure that one view performs better than the other you could take two different approaches.
-
Deterministic approach: You can make sure that all of the random variables have the same seed when trying both approaches to see if there is really a difference in training.
Here you can read more about it. For this simple approach I think it would be enough to set torch.manual_seed(0) before creating your net. This way the weights of your linear layer are the same for both cases.
-
Many repetitions: You could also just try a bunch of times with both views and see if you get significantly better results with one than with the other.
If the results do show that one view is better than the other, then I do not know what might be happening.
Please let me know what you find out.