Test (Nature images: Intel Image Classification | Kaggle)
Experiment 1.1: ImageNet Custom Stats vs None
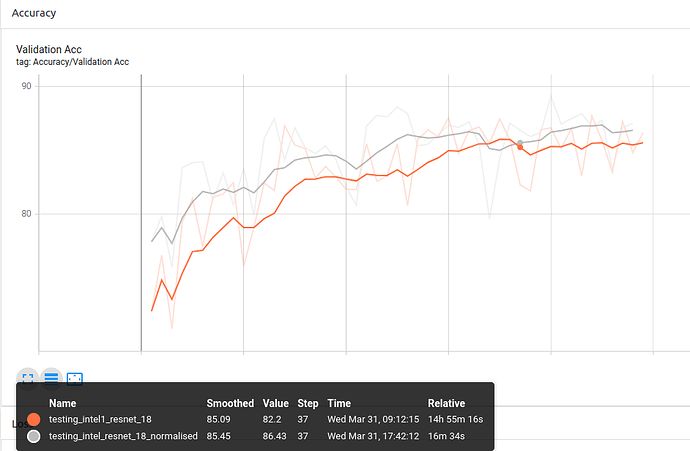
ResNet-18:
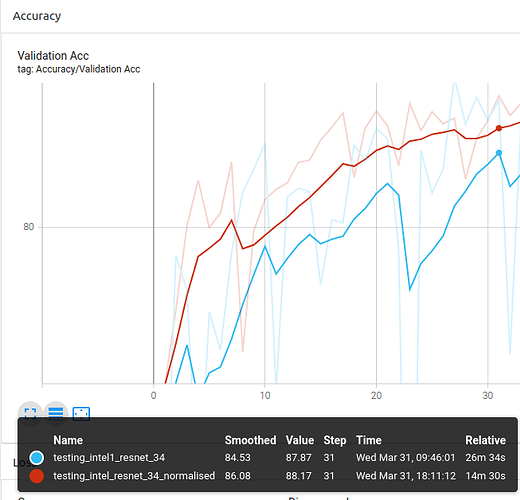
ResNet-34:
You can see the general trend being that the normalised experiments are slightly above the experiment without normalisation most of the epochs.
Conclusion 1: Using custom ImageNet stats for the pytorch pretrained models provides better results than without normalisation as it is trained on ImageNet.
Experiment 1.2: ImageNet Custom Stats vs Own Custom Stats
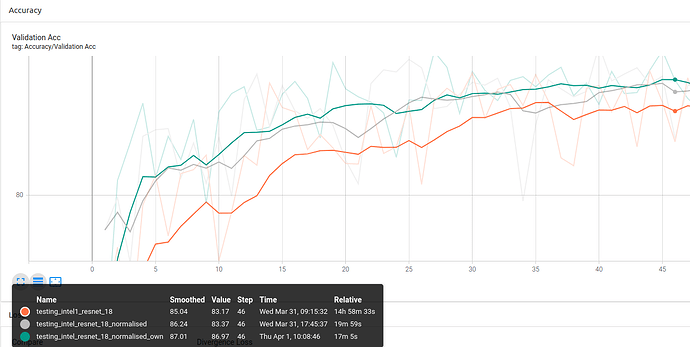
ResNet-18:
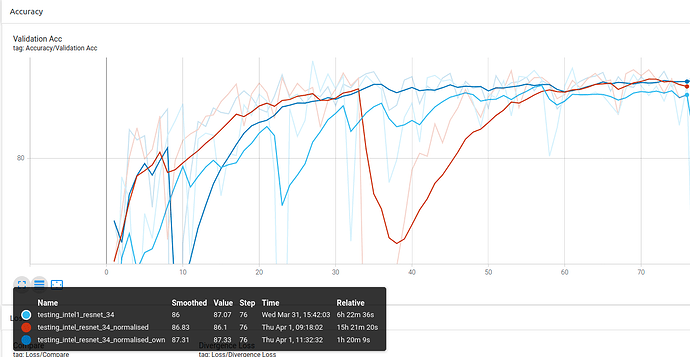
ResNet-34 (Unstable, need to go more epochs to smooth out the accuracy):
Conclusion 2: Using your own dataset stats gives better result.
For further experiments into other domains like medical images and stock technical charts photos, I think it is unnecessary as it is obvious to me that your own dataset custom stats will be superior.
Personal Opinion: Just always find your own dataset mean and standard deviation, normalise accordingly. Keep this as a common practice. It only takes roughly 5 minutes to write the script and run it.