distributions.Categorical fails with constraint.Simplex but manual check passes

1

Hey,

I am trying to instantiate a Categorical, but for some reason, in the early stages of the training it sometimes fails with

ValueError: Expected parameter probs (Tensor of shape (64, 1600)) 
of distribution Categorical(probs: torch.Size([64, 1600])) to satisfy the 
constraint Simplex(), but found invalid values:

however, if I then check the values with

torch.distributions.constraints.simplex.check(p)

I get all True.
Is it in fact another validation and the error message is misleading? An idea how to debug this?

Cheers,
Lucas

2

Hi Lucas!

I cannot reproduce your issue. (I agree that this is unexpected behavior.)

Are you able to put together a short, runnable script that reproduces this?
Perhaps you could hold on to a copy of your probs tensor, wrap your
attempted instantiation of Categorical in a try block, and print out the
fishy probs tensor (with adequate precision to reproduce the issue) if the
ValueError is raised.

What is the dtype of your probs tensor (float, double, etc.)?

Also, could you tell us what version of pytorch you are using, and if you
are seeing this on a gpu, what model it is?

(As an aside, it is perfectly possible for simplex.check() to fail but for
the instantiation of Categorical to succeed – the opposite of your issue.
This is because Categorical normalizes the sum of each row of probs
to one before applying simplex.check().)

Best.

K. Frank

3

Hey @KFrank,

thanks for the quick response. I dumped the tensor in a try except block. I uploaded it here:
https://oc.embl.de/index.php/s/IxhtqcoNbUnpLVS

and the behaviour on my machine as

image
image1964×1010 135 KB

The relevant parts of my environment are:

Name Version Build Channel

cudatoolkit 11.3.1 h9edb442_10 conda-forge
python 3.10.5 h582c2e5_0_cpython conda-forge
python_abi 3.10 2_cp310 conda-forge
pytorch 1.12.0 py3.10_cuda11.3_cudnn8.3.2_0 pytorch
pytorch-lightning 1.6.5 pypi_0 pypi
pytorch-mutex 1.0 cuda pytorch

complete env here: https://oc.embl.de/index.php/s/UwFFBFDJy6s71t0

4

Hi Lucas!

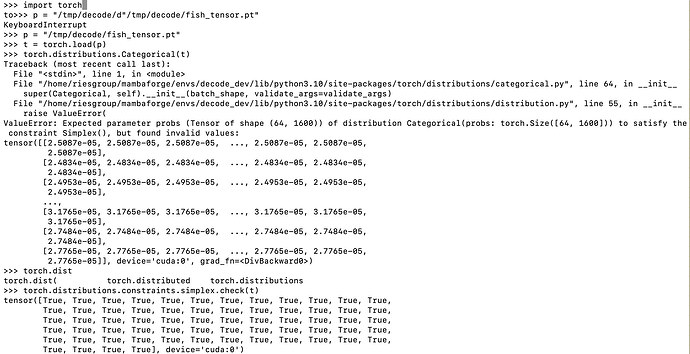
I can reproduce your issue using your fishy_tensor.

I believe that it is caused by a somewhat unlikely conspiracy of round-off
error, likely exacerbated by the fact that the rows of your probs tensor
are rather long (length 1600).

In your case your probs (fishy_tensor) are proper probabilities, with rows
normalized to sum to one (and it passes simplex.check()). Categorical
does not require its row-sums to be normalized to one, so it normalizes
them (in your case, redundantly, but Categorical doesn’t know this) before
it applies. simplex.check(). The normalization that Categorical applies
changes the round-off error a little bit and just happens to push one of the
row-sums a little bit over simplex.check()'s tolerance of 1.e-6, causing
Categorical to raise the error due to its internal call to simplex.check().

This script that uses your fishy_tensor illustrates these points:

import torch
print (torch.__version__)
print (torch.version.cuda)
print (torch.cuda.get_device_name())

fishy = torch.load ('fishy_tensor.pt')

print ((fishy.sum (dim = 1) - 1.0).abs().max())                       # rows sum to one (up to round-off)
print (torch.distributions.constraints.simplex.check (fishy).all())   # passes test

fishy_norm = fishy / fishy.sum (dim = 1).unsqueeze (-1)               # "normalize" rows to sum to one
print ((fishy_norm.sum (dim = 1) - 1.0).abs().max())                  # rows sum not quite as well to one
print (torch.distributions.constraints.simplex.check (fishy_norm))    # fails
print ((fishy_norm.sum (dim = 1) - 1.0).abs() > 1.e-6)                # simplex uses 1.e-6 as its tolerance

print (fishy_norm.sum (dim = 1)[45] - 1.0)                            # row 45 is the culprit
print (fishy_norm[45].sum() - 1.0)                                    # but details of cuda sum matter

And here is its output:

1.12.0
11.6
GeForce GTX 1050 Ti
tensor(7.1526e-07, device='cuda:0', grad_fn=<MaxBackward1>)
tensor(True, device='cuda:0')
tensor(1.0729e-06, device='cuda:0', grad_fn=<MaxBackward1>)
tensor([ True,  True,  True,  True,  True,  True,  True,  True,  True,  True,
         True,  True,  True,  True,  True,  True,  True,  True,  True,  True,
         True,  True,  True,  True,  True,  True,  True,  True,  True,  True,
         True,  True,  True,  True,  True,  True,  True,  True,  True,  True,
         True,  True,  True,  True,  True, False,  True,  True,  True,  True,
         True,  True,  True,  True,  True,  True,  True,  True,  True,  True,
         True,  True,  True,  True], device='cuda:0')
tensor([False, False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False, False, False, False,
        False, False, False, False, False,  True, False, False, False, False,
        False, False, False, False, False, False, False, False, False, False,
        False, False, False, False], device='cuda:0')
tensor(-1.0729e-06, device='cuda:0', grad_fn=<SubBackward0>)
tensor(-5.9605e-07, device='cuda:0', grad_fn=<SubBackward0>)

For what it’s worth, running your particular fishy_tensor on my cpu does not
show this behavior.

I assume that your code calls simplex.check() to protect against Categorical
raising an error. If you’re comfortable that your probs vector is legit, you could
instantiate Categorical with validate_args = False. (If you want to stick
with the validation and call simplex.check() for protection, I imagine that
(redundantly) normalizing your probs tensor (to mimic what Categorical does
internally) before making your call to simplex.check() might be an adequate
work-around.)

I also note – not that I think that you should read anything into this – summing
row 45 of fishy_tensor (after normalizing it) in isolation does not cross
simplex.check()'s 1.e-6 tolerance, while summing it as a row sum of the
whole tensor does. I assume that this causes a slight difference in innocent
round-of error due to the gpu using differing orders of operations in the two
cases.

I don’t really see this as a bug, but rather an “expected” consequence
of round-of error. One could argue, however, (and I suppose I do) that
Categorical / simplex.check() should take into account the length
of the probability vectors and widen out the tolerance as they become
longer.

Best.

K. Frank

5

Thanks for looking into that! Yes indeed the workaround is easy, I was already considering setting the validation to false, but I wanted to know what was going on.
I can understand how this comes about; not sure whether this should be considered a bug.
I guess if the class which itself applies the normalization induces the rounding error, it should be considered a bug, no?
Maybe I should raise a GH issue, don’t know.

6

Hi Lucas!

A bit of an update: So far, I have only been able to reproduce your issue
using your fishy tensor on my gpu. I’ve tried various schemes to reproduce
it using random data (and lots of trials) without success.

I would say that this is legitimately a bug (but maybe a minor edge case).
I think your logging a github issue would be appropriate. If you do, be sure
to attach your fishy tensor so that it can be reproduced.

Based on my (failed) experiments, I am less convinced by my original
theory of unlikely, but straightforward round-off error (although that
theory could still be true).

If it is round-off error, I would say that there is a (minor) bug in
simplex.check(). Perhaps simplex.check() should widen out
its tolerance based on the length of the rows of the probs tensor.

But if straightforward round-off error doesn’t explain the issue, this would
hint at a possible cuda bug – not that I have any idea what it could be.

Is there any chance that you could capture another distinct fishy tensor?
If it’s not just round-off error, having more examples that reproduce it would
likely be a big help in tracking down what is going on.

@ptrblck: This seems to me to be a weird one – would you want to take
a look?

Best.

K. Frank

7

Thanks for pinging me on this issue.
Could you also post which PyTorch release you’ve used to reproduce the issue, please?

@Haydnspass did you already create a GitHub issue? Also, were you seeing the same issue using the latest nightly binary?

8

@ptrblck yep I opened the GH issue Categorical fails simplex validation after its own normalisation on CUDA · Issue #87468 · pytorch/pytorch · GitHub after @KFrank could reproduce the issue. Maybe the discussion should go move there?
I posted the environment above, it should be pytorch 1.12.0 py3.10_cuda11.3_cudnn8.3.2_0 pytorch
I will try the latest binary :slight_smile:

9

Hi @ptrblck (and Lucas)!

For completeness:

I reproduce the issue (solely with the fishy_tensor) on pytorch 1.12.0 /
cuda 11.6 / gpu GeForce GTX 1050 Ti.

I also reproduced the issue on a version-1.14 nightly build from when I
responded earlier, namely pytorch 1.14.0.dev20221014 / cuda 11.7 /
gpu GeForce GTX 1050 Ti.

Best.

K. Frank

10

I got exactly the same issue with torch 1.13.0, torchaudio 0.12.1, torchvision 0.13.1, cuda 12.1. I tried different GPUs including A100, 4090, 3080ti, 3070. I can reproduce the issue every time.

11

Hello! I solved it in the next way.

from torch.distributions import Distribution
Distribution.set_default_validate_args(False)

if in your code one python instance you could use flag python -O
But if there are many python instances like in RLLib distributions, you need to turn off validation in custom class definition (or before usage torch distributions)