Hello. Can somebody help me to figure out is it normal behaviour of model or not:
I have a model with GRUCell in it. I’m using it in RL setting, so I’m feeding it input data one sample at a time (no batches, no tensors for sequence, just separate 1xN tensors for input points in loop)
And I have two identical (?) ways of calculating loss:
for i_episode in range(max_episodes):
sim = Sim()
sim.run(max_iters, model)
loss = model.loss()
loss.backward()
model.reset_train_data()
if i_episode % update_episode == 0 and i_episode != 0:
optimizer.step()
optimizer.zero_grad()
(That is every training episode I calculate loss across some sim iterations (<=max_iters), then backprop it, accumulating gradients and every update_episode use it in optimizer, zeroing it afterwards.
The other way is this:
loss = torch.tensor([0.0])
for i_episode in range(max_episodes):
sim = Sim()
sim.run(max_iters, model)
loss += model.loss()
model.reset_train_data()
if i_episode % update_episode == 0 and i_episode != 0:
loss.backward()
optimizer.step()
optimizer.zero_grad()
loss = torch.tensor([0.0])
(Accumulate sum of losses across update_episode episodes, then backpropagate it)
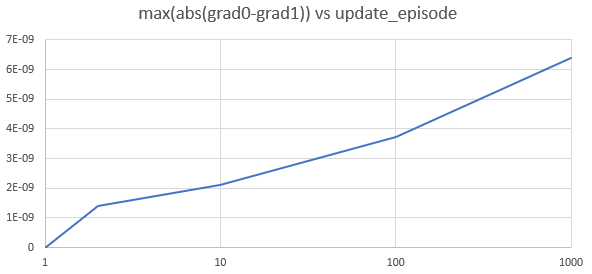
It should give the same result, I suppose, but resulting gradients differs ( (grad0-grad1).abs().max() is 1.00000e-04 * 1.1635).
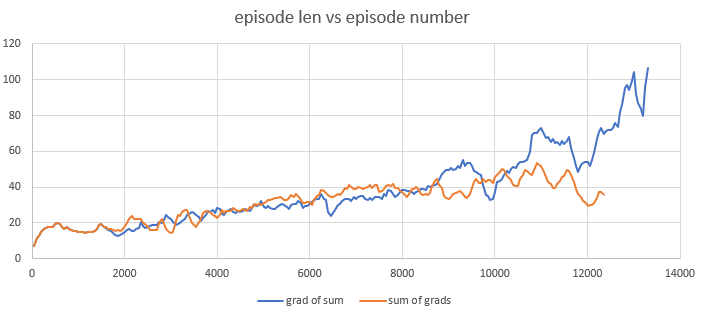
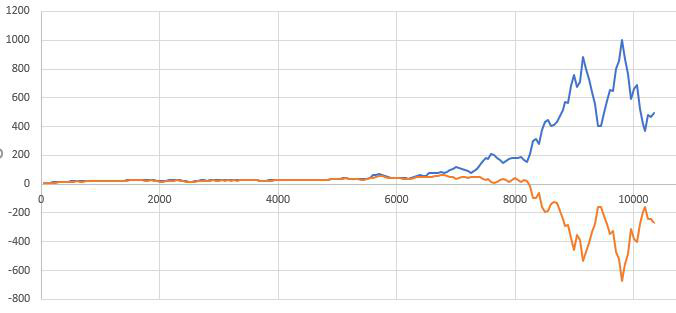
After 100-200 updates this cause serious divergence in weigths of models trained first and second ways.
It can be be result of rounding erros, but 10^-4 seems to be to much for such kind of error. Also first approach to calculating gradient seems to have poor convergence, while second converges better, but has long autograd graph dependencies, that slows calculations and sometimes causes stack overflows.
Any thoughts?
Thanks!