Hi, I am using Pytorch to reproduce the results of the 1D linear advection problem in this paper. The problem is quite simple. I am not however able to reproduce the results using the given settings : a fully connected NN with 2 hidden layers each with 10 hidden units, sigmoid activation function and a mixed dynamic training using both SGD and L-BFGS optimizers:
we have implemented the gradients according to the schemes presented in the
previous section and we consequently use the BFGS method
with default settings from SciPy to train the ANN.An issue one might encounter is that the line search in BFGS
fails due to the Hessian matrix being very ill-conditioned. To circumvent this we use a BFGS in combination with stochastic gradient descent. When BFGS fails due to line search failure we run
1000 iterations with stochastic gradient descent with a very small learning rate, in the order of 10−9, to bring BFGS out of the troublesome region. This procedure is repeated until convergence or until the maximum number of allowed iterations has been exceeded
I would like to know how I can implement their dynamic training approach in Pytorch. I just managed to first pre train the model using SGD for n iterations and then train it using L-BFGS until it converges. something like:
def loss_LBFGS(self):
# operations to calculate the loss
self.optimizer_LBFGS.zero_grad()
loss.backward()
return loss
def train(self, n_iteration_sgd):
self.ann_u.train()
# *****************************************************************************
# pretrain with the SGD optimizer
for i in range(n_iteration_sgd):
# the same operations to calculate the loss
self.optimizer_sgd.zero_grad()
loss.backward()
self.optimizer_sgd.step()
# *****************************************************************************
# training using the LBFGS optimizer
self.optimizer_LBFGS.step(self.loss_LBFGS)
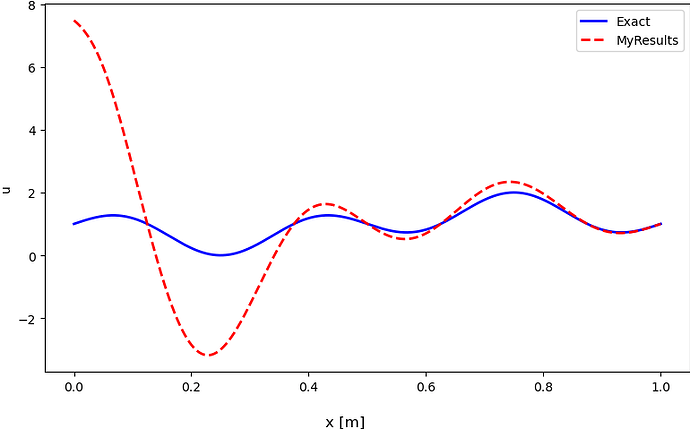
But this is not exactly what they do. The results that I get using my train function are shown in the following figure:
I think the problem comes from my training approach that is not fully correct. I would appreciate any help. Thank you.