I’m playing with simplified Wasserstein distance (also known as earth mover distance) as the loss function for N classification task. Since the gnd is a one-hot distribution, the loss is the weighted sum of the absolute value of each class id minus the gnd class id.

p_i is the softmax output.
It is defined as follows:
class WassersteinClass(nn.Module):
def __init__(self) -> None:
super().__init__()
def forward(self, likelihood, gnd_idx):
batch_size = 1
l = likelihood.shape[1] # number of bins 100
gnd_idx = gnd_idx.reshape((batch_size, 1))
idxs = torch.arange(0, l, dtype=torch.float32).to(device=config.device, non_blocking=True)
batch_idxs = idxs.repeat(batch_size, 1)
D = torch.abs(batch_idxs-gnd_idx) # broadcast
loss = torch.sum(likelihood*D)
return loss
Now I noticed that the gradient vanishes so I want to check its gradient regarding softmax input by creating a toy example. In this example, gnd (4) is one-hot and likelihood is nearly one-hot (peak at 2).
criterion = WassersteinClass()
# check gradient of softmax input
gnd_idx = torch.full([1], 4)
likelihood = torch.ones(1, 5)*1e-3
likelihood[:, 2] = 100
likelihood.requires_grad_()
softmax = nn.Softmax(1)
prob = softmax(likelihood)
prob.requires_grad_()
print('sfotmax output:', prob)
prob.retain_grad()
>>>sfotmax output: tensor([[3.7835e-44, 1.0089e-43, 1.0000e+00, 3.7835e-44, 3.7835e-44]],
grad_fn=<SoftmaxBackward0>)
wass = criterion(prob, gnd_idx)
print('loss:', was)
>>> loss: tensor(2., grad_fn=<SumBackward0>)
Its gradient regarding softmax output is quite neat.
b = prob.grad
print('loss gradient after softmax:', b)
>>>loss gradient after softmax: tensor([[4., 3., 2., 1., 0.]])
The gradient of softmax input from autograd:
a = torch.autograd.grad(wass, [likelihood])
print('loss gradient before softmax:', a) # the gradient is the distance to gnd
>>> loss gradient before softmax: (tensor([[ 7.5670e-44, 1.0089e-43, 0.0000e+00, -3.7835e-44, -7.5670e-44]]),)
According to the chain rule of backpropagation
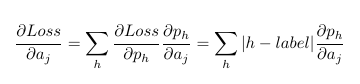

# gradient of loss regarding softmax input a[i]
for i in range(5):
grad_softmax = -prob[:, i]*prob
grad_softmax[:, i] = prob[:, i] * (1-prob[:, i])
print(f'grad L/a{i}:{torch.sum(b*grad_softmax)}')
>>>grad L/a0:7.567011707354012e-44
>>>grad L/a1:1.0089348943138683e-43
>>>grad L/a2:-4.918557609780108e-43 !!!!!!!!!!Different
>>>grad L/a3:-3.783505853677006e-44
>>>grad L/a4:-7.567011707354012e-44
All of the gradients are correct except L/a2, which is Wasserstein distance regarding the second input of softmax. Why does this happen?