Extract features from parts

vision
1

if I have an image that is split into several parts and I need to extract features from them as a whole image… I mean, for example, the original image is a dog at the beach … this picture is divided into three parts “beach, sea, dog”. is there any way to extract features for those parts as one image? does concatenate features will be the same feature as the original image

3

I think summing is what you want, and here’s a quick experiment that shows that it probably works, but it may not be trivial:

import torch, torchvision
from torchvision.transforms import ToTensor, FiveCrop, Normalize, ToPILImage
img = Image.open("cat.jpg").resize((224, 224))
device = torch.device("cuda")

n = lambda x: Normalize(0.50, 0.25)(x)
tensor_big = n(ToTensor()(img)).to(device)  # the overall image
tensors_parts = [n(ToTensor()(x)).to(device) for x in FiveCrop(224//2)(img)[:-1]]  # image divided into 4

net = torch.hub.load('pytorch/vision:v0.10.0', 'resnet50', pretrained=True)
net.fc = torch.nn.Sequential()  # eliminate classification layer
net.to(device)

ToPILImage()(torchvision.utils.make_grid(tensor_big))

image

ToPILImage()(torchvision.utils.make_grid(tensors_parts))

image

Let’s analyze how correlated the following two features are:

  • features extracted from the overall image
  • features extracted from each of the quarters of the image, and then summed
features_big = net(tensor_big.unsqueeze(0)).squeeze()
features_parts = net(torch.stack(tensors_parts))
x = features_parts.sum(dim=0).cpu().detach().numpy()
y = features_big.cpu().detach().numpy()
plt.scatter(x, y)
plt.title(f"correlation = {100 * np.corrcoef(x, y)[0, 1]:.0f}%")
plt.xlabel("features of the parts, summed")
plt.ylabel("features of the overall image")

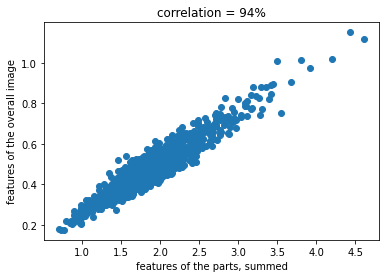
image

94% correlation seems pretty high, however this could be driven by network weights or something. Let’s run an experiment where we generate random images and see how much correlation those yield, so we can opine on whether 94% is especially high or not:

n_simulations = 1000
corrcoeffs = []
for _ in range(n_simulations):
    z = net(torch.randn(3, 224, 224).unsqueeze(0).to(device)).squeeze().cpu().detach().numpy()
    corrcoeffs.append(np.corrcoef(z, y)[0, 1])
plt.hist(corrcoeffs, bins=20);

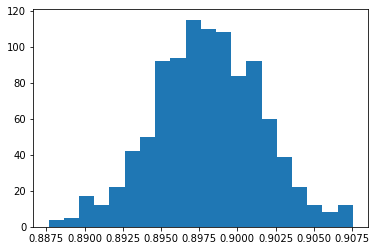
image

This suggests that, at least as far as images generated from random pixels are concerned, we have the following results:

  • the “baseline” correlation between noise-generated features and our features is also very high, at around 90%
  • however, 94% is significantly stronger than this baseline, the maximum achieved in 1000 random sims being < 91%

So I would weakly conclude from this that summing the features extracted from parts is a promising approach.

Would be curious if others have thoughts on this.

1 Like
4

great explanation , thanks a lot