Hi,
I’d like to find an index of the biggest value in the array that smaller than my provided number.
In this array, I will have more than 2 values.
Example:
val = 0.25
arr = [0, 0.1, 0.2, 0.4, 0.42, 0.5, 0.56, 1]
result = my_func(arr, val)
So the first smaller value is 0.2 and
result = 2
Right now I’m doing it with python implementation of binary search. But I think there is some faster approach for PyTorch.
Because it’s a huge bottleneck for me.
Maybe it’s similar to MaxPool implementation, but I don’t really know.
Thank you,
Tim
Wouldn’t 0 be the first smaller number in the array?
How are you calculating the method at the moment?
Yes, thanks - I’ve changed the description of the issue.
I need an index of the biggest value in the array that is smaller than my provided value.
Right now I’m using binary search.
I’m using this Python module from the standard library:
https://docs.python.org/3/library/bisect.html
for binary search. Method - bisect. bisect_left.
Example of usage:
from bisect import bisect_left
nuclears = [0, 0.1, 0.15, 0.2, 0.3, 0.33, 0.5, 0.51, 0.8, 1]
x = 0.505
idx = bisect_left(nuclears, x)
idx
7
But I need to do this operation a lot of times and it slows me down.
As the order of array is already ascending, so you can try this:
import torch
val = 0.505
nuclears = [0, 0.1, 0.15, 0.2, 0.3, 0.33, 0.5, 0.51, 0.8, 1]
mat = torch.Tensor(nuclears)
print(mat > val)
mat_tmp = torch.min((mat > val), 0)
print(mat_tmp[1].item() + 1)
1 Like
Nice approach.
I wrote a small benchmark:
def comparing_idx_search_methods():
import random
import time
def bisect_search(nuclears, x):
idx = bisect_left(nuclears, x)
return idx
def pytorch_search(nuclears, x):
mat_tmp = torch.min((nuclears > x), 0)
return mat_tmp[1].item() + 1
number_of_iterations = 100000
nuclears = [0, 0.1, 0.15, 0.2, 0.3, 0.33, 0.5, 0.51, 0.8, 1]
x_s = [random.random() for _ in range(number_of_iterations)]
start = time.time()
for val in x_s:
idx = bisect_search(nuclears, val)
end = time.time()
execution_time = end - start
print("bisect: {} seconds".format(round(execution_time, 2)))
start = time.time()
nuclears = torch.Tensor(nuclears)
for val in x_s:
idx = pytorch_search(nuclears, val)
end = time.time()
execution_time = end - start
print("pytorch: {} seconds".format(round(execution_time, 2)))
and basic output is:
bisect: 0.06 seconds
pytorch: 2.17 seconds
Of course - the reason is that bisect uses binary search and does not run through all elements.
But it was a nice try - I thought maybe pytorch uses something under the hood and it would be faster.
I think maybe the solution has to be connected with how maxpool works but I don’t know where to dig next.
from bisect import bisect_left
import torch
import torch.nn.functional as F
def comparing_idx_search_methods():
import random
import time
def bisect_search(nuclears, x):
idx = bisect_left(nuclears, x)
return idx
def pytorch_search(nuclears, x):
tmp_feat = 1/ (1 + F.relu(nuclears - x))
mat_tmp = torch.max(tmp_feat, dim=1)
return mat_tmp[1] + 1
number_of_iterations = 1000000
nuclears = [0, 0.1, 0.15, 0.2, 0.3, 0.33, 0.5, 0.51, 0.8, 1]
x_s = [random.random() for _ in range(number_of_iterations)]
start = time.time()
for val in x_s:
idx = bisect_search(nuclears, val)
end = time.time()
execution_time = end - start
print("bisect: {} seconds".format(round(execution_time, 2)))
start = time.time()
nuclears = torch.Tensor(nuclears).view(1, -1)
x_s_th = torch.Tensor(x_s).view(-1, 1)
idx_th = pytorch_search(nuclears, x_s_th)
# for val in x_s:
# idx = pytorch_search(nuclears, val)
end = time.time()
execution_time = end - start
print("pytorch: {} seconds".format(round(execution_time, 2)))
comparing_idx_search_methods()
Just a few modifications, making it computing-parallel. Now, it surpasses normal for-loop in numpy.
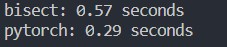
5 Likes