Hello,
I am working on a CNN based classification.
I am using torchvision.ImageFolder to set up my dataset then pass to the DataLoader and feed it to
pretrained resnet34 model from torchvision.
I have a highly imbalanced dataset which hinders model performance.
Say ‘0’: 1000 images, ‘1’:300 images.
I know I have two broad strategies: work on resampling (data level) or on loss function(algorithm level).
I first tried to change the cross entropy loss to custom FocalLoss. But somehow I am getting even worse performance like below:
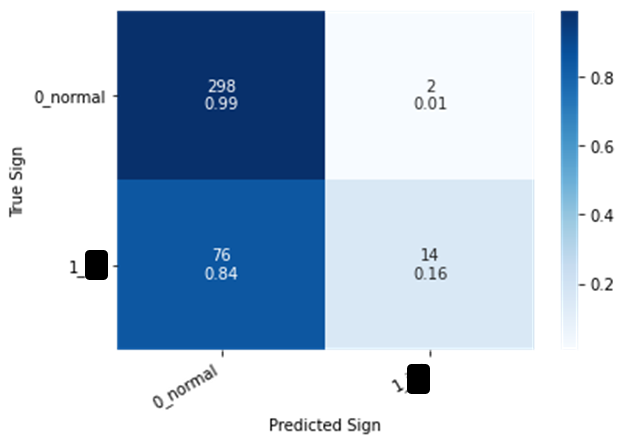
my training function looks like this can anybody tell me what I am missing out or doing wrong?
def train_model(model, data_loaders, dataset_sizes, device, n_epochs=20):
optimizer = optim.Adam(model.parameters(), lr=0.0001)
scheduler = lr_scheduler.StepLR(optimizer, step_size=30, gamma=0.1)
loss_fn = FocalLoss().to(device)
history = defaultdict(list)
best_accuracy = 0
for epoch in range(n_epochs):
print(f'Epoch {epoch + 1}/{n_epochs}')
print('-' * 10)
train_acc, train_loss = train_epoch(
model,
data_loaders['train'],
loss_fn,
optimizer,
device,
scheduler,
dataset_sizes['train']
)
print(f'Train loss {train_loss} accuracy {train_acc}')
val_acc, val_loss = eval_model(
model,
data_loaders['val'],
loss_fn,
device,
dataset_sizes['val']
)
print(f'Val loss {val_loss} accuracy {val_acc}')
print()
history['train_acc'].append(train_acc)
history['train_loss'].append(train_loss)
history['val_acc'].append(val_acc)
history['val_loss'].append(val_loss)
if val_acc > best_accuracy:
torch.save(model.state_dict(), 'best_model_state.bin')
best_accuracy = val_acc
print(f'Best val accuracy: {best_accuracy}')
model.load_state_dict(torch.load('best_model_state.bin'))
return model, history
The custom FocalLoss function from the web looks like below (sorry, I forgot the reference):
class FocalLoss(nn.Module):
#WC: alpha is weighting factor. gamma is focusing parameter
def __init__(self, gamma=0, alpha=None, size_average=True):
#def __init__(self, gamma=2, alpha=0.25, size_average=False):
super(FocalLoss, self).__init__()
self.gamma = gamma
self.alpha = alpha
if isinstance(alpha, (float, int)): self.alpha = torch.Tensor([alpha, 1 - alpha])
if isinstance(alpha, list): self.alpha = torch.Tensor(alpha)
self.size_average = size_average
def forward(self, input, target):
if input.dim()>2:
input = input.view(input.size(0), input.size(1), -1) # N,C,H,W => N,C,H*W
input = input.transpose(1, 2) # N,C,H*W => N,H*W,C
input = input.contiguous().view(-1, input.size(2)) # N,H*W,C => N*H*W,C
target = target.view(-1, 1)
logpt = F.log_softmax(input, dim=1)
logpt = logpt.gather(1,target)
logpt = logpt.view(-1)
pt = logpt.exp()
if self.alpha is not None:
if self.alpha.type() != input.data.type():
self.alpha = self.alpha.type_as(input.data)
at = self.alpha.gather(0, target.data.view(-1))
logpt = logpt * at
loss = -1 * (1 - pt)**self.gamma * logpt
if self.size_average: return loss.mean()
else: return loss.sum()