Formulation for a custom regularizer to minimize amount of space taken by weights

autograd
1

Hello all.

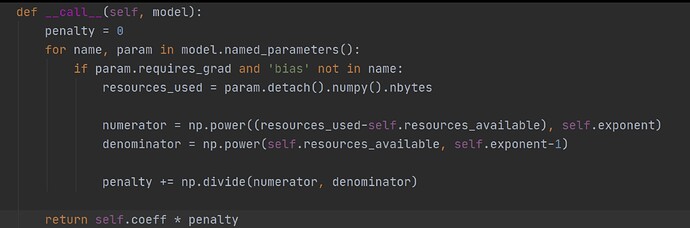
Below is a screenshot of a custom regularizer I have implemented.

The goal of this regularizer is to minimize the total number of space taken by the weights rather than affect the value of any one weight. However by the nature of a regularizer, I require a formulation for my regularizer that is weight dependent, since otherwise backdrop won’t take it into account.

Essentially, if there are too many weights, it should push all weights to zero equally, and if there are too few weights, push the value of the weights to go up.

My current formulation works but is not weight dependent. I have the function that would push towards the points intended given the number of bytes use and number of bytes available, but as said, it’s weight independent.

I appreciate any input.

PS: While I use numpy operations here, I am aware I need to use torch operations on tensors so as to remain in the computation graph. The problem is that resources_used remains a scalar, and the computations remain weight independent.

IMG_4424
IMG_44242435×807 169 KB

2

Hi,

That penalty that you compute does not depend on the value of the parameters right? So it is expected that no gradients wrt these values can be computed.

3

Exactly, so I’m looking for a formulation that does the same but is weight dependent.

4

Ho sorry I missed one paragraph in your question :confused:

Well anything related to the number of entries won’t work as it won’t be differentiable.
You can renormalize each value to get their number because that would give you a gradient of 0.
I guess you could try to center the parameter and use the standard deviation? You measure how much each tensor varies from a mean. In theory, you could represent them as a mean value and their offsets. So the closer they are, the better?

5

Perhaps L1 penalty (see here) proportional to what you compute would work?

6

Thank you for both answers have given me some ideas to think about.