Functional Derivative Discontinuity

autograd
1

Hi, I tried using Pytorch’s autograd to calculate functional derivatives. For the case of a periodic function, a=cos^2(x), I considered an integral A=\int a^6, which should have a functional derivative of dA/da = 6a^5. The code to perform it is as follows.

a = torch.tensor(np.cos(np.linspace(0, 2*np.pi, 10000, endpoint=False))**2, requires_grad=True).float()
A = torch.trapz(a**6)
b = torch.autograd.grad(A, a)[0] 
plt.plot(b, 'b', label = 'autograd')
plt.plot(6*a.detach().numpy()**5, '--r', label = 'expected')
plt.legend()
plt.show()

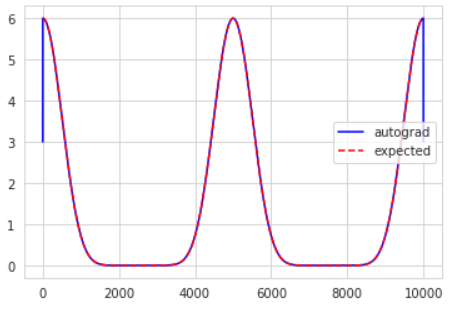
discontinuity

The expected result agrees with the autograd result for the most part, but there’s some strange behavior at the boundaries. Increasing the number of grid points for the integration doesn’t seem to make this problem go away (but I haven’t tested this extensively). After testing a few examples, I noticed that it went down to about half of the expected value at the boundaries. Does anybody have an idea of how this problem arises and how it can be fixed? Thank you!

2

It seems to be fixed by replacing the torch.trapz() with torch.sum(). The discontinuity goes away when the second line is A = torch.sum(a**6) instead. I’m still not sure why this is the case though.

3

Isn’t this due to the border condition of the trapz function?

2 Likes
4

Thanks, that’s probably the case. However, I’m still somewhat puzzled as to how I should think about it since both methods (sum and trapz) are numerical approximations to what theoretically is a continuous integral. I’m guessing this wouldn’t be a problem if I had used periodic boundary conditions and an auto-differentiable implementation of trapz that handled the boundaries correctly?