Hello,
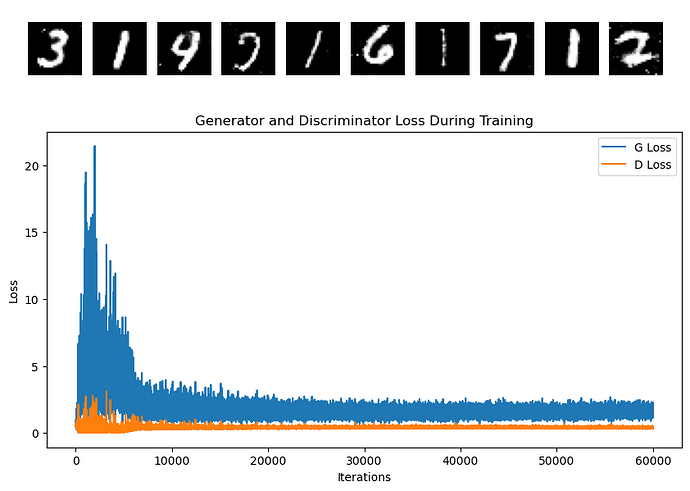
I am working on implementing a vanilla GAN on MNIST data. I followed standard vanilla GAN model but I’m encountering an issue where the d_loss and g_loss curves are not converging to an equilibrium value. Considering that MNIST is generally an easy dataset to train on, I’m puzzled as to why my GAN training isn’t reaching the optimal point. I’m wondering if there might be a mistake in my Pytorch code.
Could anyone who has successfully trained a GAN model on MNIST data share their insights or experiences?
Appreciate the help in advance
Below is my simulation code and the resulting loss curves:
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
import torchvision.datasets as datasets
import matplotlib.pyplot as plt
import numpy as np
from datetime import datetime
device = torch.device("cuda" if torch.cuda.is_available() else "cpu") # Set device
# Hyperparameters
latent_size = 100
hidden_size = 256
image_size = 784 # 28x28
num_epochs = 100
batch_size = 100
learning_rate = 0.0002
# MNIST dataset
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(mean=[0.5], std=[0.5])
])
train_dataset = datasets.MNIST(root='./data', train=True, transform=transform, download=True)
train_loader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True) # type: ignore
# Discriminator
class Discriminator(nn.Module):
def __init__(self):
super(Discriminator, self).__init__()
self.model = nn.Sequential(
nn.Linear(image_size, 4*hidden_size),
nn.LeakyReLU(0.2),
nn.Linear(4*hidden_size, 2*hidden_size),
nn.LeakyReLU(0.2),
nn.Linear(2*hidden_size, hidden_size),
nn.LeakyReLU(0.2),
nn.Linear(hidden_size, 1),
nn.Sigmoid()
)
def forward(self, x):
x = x.view(x.size(0), -1)
output = self.model(x)
return output
# Generator
class Generator(nn.Module):
def __init__(self):
super(Generator, self).__init__()
self.model = nn.Sequential(
nn.Linear(latent_size, hidden_size),
nn.ReLU(True),
nn.Linear(hidden_size, 2*hidden_size),
nn.ReLU(True),
nn.Linear(2*hidden_size, 4*hidden_size),
nn.ReLU(True),
nn.Linear(4*hidden_size, image_size),
nn.Tanh()
)
def forward(self, z):
output = self.model(z)
output = output.view(output.size(0), 1, 28, 28)
return output
# Create the models
D = Discriminator().to(device)
G = Generator().to(device)
# Loss and optimizer
criterion = nn.BCELoss()
d_optimizer = optim.Adam(D.parameters(), lr=learning_rate, betas=(0.5, 0.999))
g_optimizer = optim.Adam(G.parameters(), lr=learning_rate, betas=(0.5, 0.999))
g_losses = []
d_losses = []
# Training loop
for epoch in range(num_epochs):
for i, (images, _) in enumerate(train_loader):
# Prepare real and fake data
real_images = images.to(device)
real_labels = torch.ones(batch_size, 1).to(device)
fake_labels = torch.zeros(batch_size, 1).to(device)
# Train Discriminator
outputs = D(real_images)
d_loss_real = criterion(outputs, real_labels)
real_score = outputs
z = torch.randn(batch_size, latent_size).to(device)
fake_images = G(z)
outputs = D(fake_images.detach())
d_loss_fake = criterion(outputs, fake_labels)
fake_score = outputs
d_loss = (d_loss_real + d_loss_fake)/2
d_optimizer.zero_grad()
d_loss.backward()
d_optimizer.step()
# Train Generator
z = torch.randn(batch_size, latent_size).to(device)
fake_images = G(z)
outputs = D(fake_images)
g_loss = criterion(outputs, real_labels)
g_optimizer.zero_grad()
g_loss.backward()
g_optimizer.step()
g_losses.append(g_loss.item())
d_losses.append(d_loss.item())
if (i+1) % 600 == 0:
print(f'Epoch [{epoch+1}/{num_epochs}], Step [{i+1}/{len(train_loader)}], d_loss: {d_loss.item():.4f}, g_loss: {g_loss.item():.4f}, D(x): {real_score.mean().item():.2f}, D(G(z)): {fake_score.mean().item():.2f}')
# Save some generated images
z = torch.randn(batch_size, latent_size).to(device)
fake_images = G(z)
fake_images = fake_images.view(fake_images.size(0), 28, 28)
fake_images = fake_images.data.cpu().numpy()
plt.figure(figsize=(10, 10))
for i in range(10):
plt.subplot(10, 10, i+1)
plt.imshow(fake_images[i], cmap='gray')
plt.axis('off')
current_time = datetime.now().strftime("%Y%m%d-%H%M%S")
plt.savefig('figs/MNIST_samples_{current_time}.png', bbox_inches='tight')
plt.show()
plt.figure(figsize=(10, 5))
plt.title("Generator and Discriminator Loss During Training")
plt.plot(g_losses, label="G Loss")
plt.plot(d_losses, label="D Loss")
plt.xlabel("Iterations")
plt.ylabel("Loss")
plt.legend()
current_time = datetime.now().strftime("%Y%m%d-%H%M%S")
plt.savefig(f'figs/MNIST_gan_loss_plot_{current_time}.png', bbox_inches='tight')
plt.show()