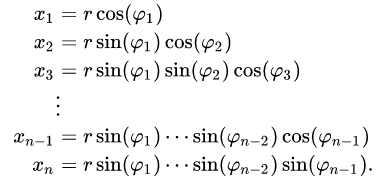Generating vector on an n-sphere

[denvercoder9]

Hi:)

Is there an efficient way to create an unit vector on an n-sphere from n-1 parameters? That is I want to implement these equations (taken from wikipedia.org/wiki/N-sphere):

with r=1 s.t. I can use the result with autograd w.r.t. phi. The fact that I want to use autograd might be a constraint since one has to pay attention if vector elements are overwritten…

Currently I am using softmax on n parameters which is not equivalent to the unit vector on n-sphere approach since there is one additional degree of freedom. The problem is that my NN occasionally generates extremely small and large values for all n parameters which is not penalize in my loss function due to the normalization of the softmax function. (The magnitude of the vector of the n parameters does not play a role in the loss function.)

Any suggestions?

Thanks for your help!

[KFrank]

Hi Denver!

@denvercoder9

Is there an efficient way to create an unit vector on an n-sphere from n-1 parameters?

First a brief word on mathematical terminology: A n-sphere is
described by n (independent) parameters and is often thought
of as being embedded in (n+1)-space.

So a 2-sphere is the (two-dimensional) surface of a three-dimensional
ball (embedded in 3-space). A 1-sphere is just the ordinary circle.

That is I want to implement these equations

You most likely don’t want to implement these equations because
there are many locations where they are singular. (Also, the different
parameters are rather different in character.)

For most purposes you are much better off using n+1 slightly
redundant parameters to describe an n-sphere, namely the n+1
coordinates of a point in (n+1)-space that is constrained to be a
distance of 1 away from the origin. (This constraint describes /
eliminates the redundancy.)

Currently I am using softmax on n parameters which is not equivalent to the unit vector on n-sphere approach since there is one additional degree of freedom.

Using softmax here is likely to be sub-optimal, because, among
other reasons, the “geometry” of softmax doesn’t really match well
with the geometry of a sphere.

If you want the output of your model to be an n-sphere, you should
have your model output n+1 unbounded real values (e.g., the
n+1 outputs of a final Linear layer), and then normalize that
(n+1)-dimensional vector to have unit norm. (That extra degree of
freedom that is normalized away isn’t really a problem. Networks,
in general, contain lots of redundancy.)

The problem is that my NN occasionally generates extremely small and large values for all n parameters which is not penalize in my loss function due to the normalization of the softmax function. (The magnitude of the vector of the n parameters does not play a role in the loss function.)

I suggest directly normalizing your (n+1)-dimensional output vector,
rather than passing it through softmax, but the general concept is
fully analogous.

As you say, because the norm of your (pre-normalization) vector
doesn’t enter into your loss function, there’s nothing that keeps it
from running off to infinity (or zero). But it’s easy to stabilize. Just
add a penalty like

stabilization_loss = (1.0 - output_norm**2)**2

to your total loss.

Note, you don’t care whether your stabilization_loss forces your
output vector to have a norm that is exactly (or very close to) 1 – you
just want to keep the norm from running off to infinity and becoming
singular.

Best.

K. Frank

[denvercoder9]

These are all valid points and thank you for your suggestion. Much appreciated!