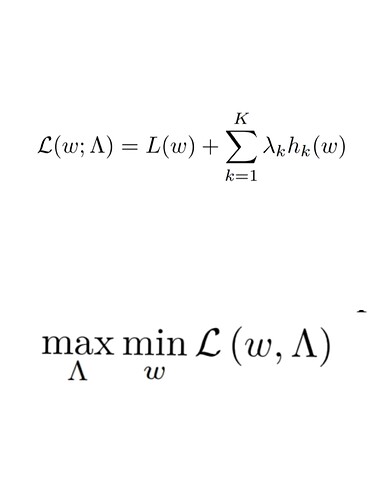Hi All,
I have a few questions related to the topic of modifying gradients and the optimizer. I’m wondering if there is an easy way to perform gradient ascent instead of gradient descent. For example, this would correspond to replacing grad_weight by -grad_weight in linear layer definition as seen in class LinearFunction(Function): from the Extending PyTorch page. My concern here is that this will mess up a downstream function that requires grad_weight instead of -grad_weight, or is this not a concern at all? A suggestion made to me was to try to modify the optimizer. Is there a simple way to go about doing W + dW instead of W - dW in the optimizer? I can’t really tell from the source code for SGD or ADAM.
Thanks for reading!