Hi! I am urgently seeking advice as I am not sure if I computed a certain gradient correctly.
Setting:
In my toy model I have a neural net called Phi_net (input data is 4d and output is 1d) and another neural net D_net (input data is 2d and output is 4d). Both have only one linear layer. I implemented them in the following way with weights initialized manually:
class Phi_Net(nn.Module):
def __init__(self):
super(Phi_Net, self).__init__()
self.fc = nn.Linear(4, 1)
with torch.no_grad():
self.fc.weight.data = torch.tensor([[1.,2.,3.,4.]])
self.fc.bias.fill_(0.)
def forward(self, x):
return self.fc(x)
class D_Net(nn.Module):
def __init__(self):
super(D_Net, self).__init__()
self.fc = nn.Linear(2, 4)
with torch.no_grad():
self.fc.bias.fill_(0)
self.fc.weight.data = torch.tensor([[1.,0.],
[0,5.],
[1.,0.],
[1.,0.]])
def forward(self, z):
return self.fc(z)
I then want to do the following: I set z = [1.,5.] and compute the squared cosine similarity between the gradient of Phi_net w.r.t. its input evaluated at x=D(z), and the partial derivative of D_net w.r.t. z_1 evaluated at z = [1.,5.]. In the toy example that is all trivial but I want to eventually do this for complexer neural nets Phi_net and D_net.
I do not know how to integrate latex into this post but I took a screenshot of the quantity that I want to compute
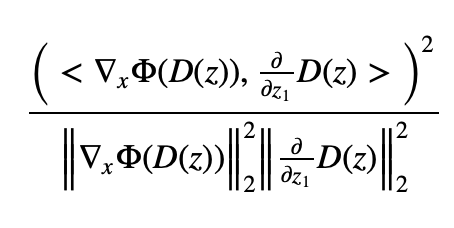
where Phi refers to the instance of the Phi_net and D to the instance of D_net. Not only do I want to compute this squared cosine similarity, I also want to compute its derivative w.r.t. to the model parameters in D_net. I tried to do this in the following code:
Phi_net = Phi_Net()
D_net = D_Net()
z = torch.tensor([1.,.5], requires_grad=True)
x = D_net(z).requires_grad_(True)
x.retain_grad()
phi = Phi_net(x)
# ------Compute squared cosine similarity----
phi.backward(retain_graph=True, create_graph=True)
dphi_dx = x.grad.clone()
print("dphi_dx: ", dphi_dx.clone().detach())
print("norm dphi_dx: ", torch.square(dphi_dx.clone().detach().norm(p=2)))
x.backward(gradient=dphi_dx,retain_graph=True, create_graph=True )
dot_prods = z.grad.clone()
print("dot_prods: ", dot_prods.clone().detach())
z.grad.zero_()
norm_sq_dD_dz = torch.zeros_like(dot_prods)
for i in range(x.shape[-1]):
unit_vec = torch.zeros(x.shape[-1], requires_grad=False)
unit_vec[i] = 1.
x.backward(gradient=unit_vec,retain_graph=True, create_graph=True)
norm_sq_dD_dz.add_(torch.square(z.grad.clone()))
z.grad.zero_()
print("norm_sq_dD_dz: ",norm_sq_dD_dz.clone().detach())
cossim_sq = torch.square(dot_prods)/ (torch.square(dphi_dx.norm(p=2))*norm_sq_dD_dz)
print("cossim_sq: ", cossim_sq.clone().detach())
D_net.fc.weight.grad.data.zero_()
# ------Compute gradient of squared cossim w.r.t weights in D_net----
cossim_sq[0].backward()
print("D_net.fc.weight.grad.data:\n", D_net.fc.weight.grad.data)
The output was
dphi_dx: tensor([1., 2., 3., 4.])
norm dphi_dx: tensor(30.0000)
dot_prods: tensor([16., 20.])
norm_sq_dD_dz: tensor([ 3., 25.])
cossim_sq: tensor([2.8444, 0.5333])
D_net.fc.weight.grad.data:
tensor([[-1.1852, 0.0000],
[ 1.4222, 0.0000],
[ 0.2370, 0.0000],
[ 0.9481, 0.0000]])
I computed the derivatives by hand and everyoutput of the above matched except for D_net.fc.weight.grad.data:, i.e. the gradient of the cossine similarity. Particularly I checked the value -1.1852 and it did not match my result.
- It looks like the squared cosine similarity was computed correctly
- But not the gradient of the squared cosine similarity w.r.t. the parameters of
D_net - I may have miscalculated my derivatives by hand though I have checked many times and
-1.1852did not match. I am not too familiar with autograd and hoped someone could look over the code to check where my mistake is (if there is indeed one) and or tell me how to compute the gradient that I want correctly and most efficiently. - Can I avoid doing my for loop
for i in range(x.shape[-1]):? I don’t thinks so but I am happy if someone has a suggestion.
Thank you so much for any help in advance!
Best
Stefan