Gradient Vanishing with Wasserstein distance

autograd
1

I’m training GoogleNet with a simplified Wasserstein distance (also known as earth mover distance) as the loss function for 100 classification problem. Since the gnd is a one-hot distribution, the loss is the weighted sum of the absolute value of each class id minus the gnd class id.
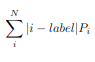
image

p_i is the softmax output.

It is defined as follows:

class WassersteinClass(nn.Module):
    def __init__(self) -> None:
        super().__init__()

    def forward(self, likelihood, gnd_idx):
        batch_size = 1
        l = likelihood.shape[1]  # number of bins  100

        gnd_idx = gnd_idx.reshape((batch_size, 1)) 
        idxs = torch.arange(0, l, dtype=torch.float32).to(device=config.device, non_blocking=True)
        batch_idxs = idxs.repeat(batch_size, 1)
        D = torch.abs(batch_idxs-gnd_idx) # broadcast
        
        loss = torch.sum(likelihood*D)
        return loss

The gradient vanishes after several epochs. I printed the output of softmax (theta), theta’s gradient, and softmax input’s gradient.

theta tensor([[0.0100, 0.0099, 0.0100, 0.0100, 0.0097, 0.0100, 0.0104, 0.0101, 0.0099,
         0.0101, 0.0103, 0.0100, 0.0097, 0.0099, 0.0102, 0.0101, 0.0099, 0.0097,
         0.0098, 0.0098, 0.0098, 0.0097, 0.0101, 0.0101, 0.0103, 0.0099, 0.0098,
         0.0098, 0.0097, 0.0098, 0.0103, 0.0098, 0.0103, 0.0101, 0.0102, 0.0097,
         0.0101, 0.0103, 0.0101, 0.0103, 0.0102, 0.0101, 0.0099, 0.0099, 0.0099,
         0.0102, 0.0103, 0.0100, 0.0099, 0.0101, 0.0103, 0.0102, 0.0100, 0.0097,
         0.0102, 0.0101, 0.0097, 0.0100, 0.0103, 0.0099, 0.0100, 0.0101, 0.0100,
         0.0099, 0.0099, 0.0102, 0.0097, 0.0103, 0.0097, 0.0097, 0.0101, 0.0103,
         0.0099, 0.0097, 0.0099, 0.0102, 0.0099, 0.0097, 0.0098, 0.0097, 0.0098,
         0.0101, 0.0102, 0.0101, 0.0103, 0.0098, 0.0099, 0.0102, 0.0100, 0.0102,
         0.0101, 0.0100, 0.0104, 0.0100, 0.0101, 0.0102, 0.0099, 0.0098, 0.0099,
         0.0097]], device='cuda:0', grad_fn=<SoftmaxBackward0>)
theta gradient before softmax tensor([[ 0.3390,  0.3260,  0.3206,  0.3079,  0.2902,  0.2891,  0.2899,  0.2720,
          0.2572,  0.2509,  0.2461,  0.2291,  0.2130,  0.2068,  0.2030,  0.1915,
          0.1780,  0.1647,  0.1557,  0.1466,  0.1360,  0.1253,  0.1206,  0.1098,
          0.1025,  0.0881,  0.0772,  0.0678,  0.0575,  0.0479,  0.0404,  0.0286,
          0.0198,  0.0093, -0.0009, -0.0105, -0.0212, -0.0318, -0.0413, -0.0524,
         -0.0623, -0.0714, -0.0800, -0.0899, -0.1002, -0.1131, -0.1246, -0.1314,
         -0.1401, -0.1525, -0.1649, -0.1741, -0.1811, -0.1844, -0.2040, -0.2134,
         -0.2137, -0.2306, -0.2483, -0.2478, -0.2603, -0.2540, -0.2403, -0.2287,
         -0.2183, -0.2148, -0.1953, -0.1969, -0.1752, -0.1655, -0.1618, -0.1556,
         -0.1391, -0.1271, -0.1194, -0.1127, -0.0995, -0.0883, -0.0796, -0.0689,
         -0.0597, -0.0512, -0.0417, -0.0312, -0.0215, -0.0107, -0.0008,  0.0093,
          0.0191,  0.0296,  0.0394,  0.0492,  0.0613,  0.0689,  0.0797,  0.0910,
          0.0985,  0.1068,  0.1174,  0.1256]], device='cuda:0')
theta gradient after softmax tensor([[60., 59., 58., 57., 56., 55., 54., 53., 52., 51., 50., 49., 48., 47.,
         46., 45., 44., 43., 42., 41., 40., 39., 38., 37., 36., 35., 34., 33.,
         32., 31., 30., 29., 28., 27., 26., 25., 24., 23., 22., 21., 20., 19.,
         18., 17., 16., 15., 14., 13., 12., 11., 10.,  9.,  8.,  7.,  6.,  5.,
          4.,  3.,  2.,  1.,  0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9.,
         10., 11., 12., 13., 14., 15., 16., 17., 18., 19., 20., 21., 22., 23.,
         24., 25., 26., 27., 28., 29., 30., 31., 32., 33., 34., 35., 36., 37.,
         38., 39.]], device='cuda:0')

What I don’t understand:

  1. Both the softmax input and output dimension is N, the theta gradient before softmax should be NN matrix. Why is it a 1N tensor here?
  2. Does the gradient vanish because of the absolute value?

The model works fine with cross-entropy loss and with the same image. Thanks for any advice!!

2

Based on your code you might be checking the scaled gradients. If you want to print the real gradients you could unscaled them first via the scaler object.

3

Thanks for the reply first!
I added scaler.unscale_(optimizer) after scaler.scale(loss).backward() and printed the gradient again. The values are still scaled by 65536.

4

Now I got it. When I removed the scaler, the gradient from backpropagation looks the same as the one from autograd. Though the problem of gradient vanishing still exists. I modified the question.