I did a Pytorch implementation for some paper (the code below), and I have an issue that I’m not able to solve.
In some runs, the NN reproduces the results reported in the paper (0.97 accuracy) and in some runs, the results are much worse (0.82).
I tried to figure out where exactly is the problem and the only thing that I found is that there is a range of seeds that bring good results (0.97) and there are some seeds that don’t. I didn’t manage to realize what exactly is the difference the only thing that I could think of is the weights initialization or that I have a bug in my code that I cant see.
The dataset I train on is MNIST
Here is my code:
class SpectralNet(nn.Module):
def __init__(self, input_dim, architecture):
super(SpectralNet, self).__init__()
self.input_dim = input_dim
self.architecture = architecture
self.layers = nn.ModuleList()
self.num_of_layers = self.architecture['num_of_layers']
current_dim = self.input_dim
for i in range(1, self.num_of_layers):
next_dim = self.architecture[f"layer{i}"]
if i == self.num_of_layers - 1:
layer = nn.Sequential(nn.Linear(current_dim, next_dim), nn.Tanh())
else:
layer = nn.Sequential(nn.Linear(current_dim, next_dim), nn.ReLU())
self.layers.append(layer)
current_dim = next_dim
self.apply(init_weights)
def forward(self, x, orthonorm_step=True):
for layer in self.layers:
x = layer(x)
if orthonorm_step:
L = torch.linalg.cholesky(torch.mm(torch.t(x), x), upper=False)
self.orthonorm_weights = np.sqrt(x.shape[0]) * torch.t(torch.inverse(L))
return torch.mm(x,self.orthonorm_weights)
class SpectralNetLoss(nn.Module):
def __init__(self):
super(SpectralNetLoss, self).__init__()
def forward(self, W, Y, normalized=False):
if normalized:
D = W.sum(1)
Y = Y / D[:, None]
Dis_y = torch.cdist(Y,Y, p=2) ** 2
return torch.sum(Dis_y*W) / (W.shape[0])
class SpectralNetOperations():
def __init__(self, model, dataset, device, siamese_net=None):
self.model = model
self.dataset = dataset
self.device = device
self.siamese_net = siamese_net
self.loss_function = SpectralNetLoss()
self.lr = SPECTRAL_HYPERPARAMS[self.dataset]["initial_lr"]
self.optimizer = optim.Adam(self.model.parameters(), lr=self.lr)
self.scheduler = optim.lr_scheduler.ReduceLROnPlateau(self.optimizer, 'min')
self.counter = 0
def ortho_step(self, x):
self.model.eval()
return self.model(x, orthonorm_step=True)
def train_step(self, x):
self.model.train()
self.optimizer.zero_grad()
Y = self.model(x, orthonorm_step=False)
if self.siamese_net is not None:
self.siamese_net.eval()
with torch.no_grad():
x = self.siamese_net.forward_once(x)
W = get_affinity_matrix(x, self.dataset).to(self.device)
loss = self.loss_function(W, Y)
loss.backward()
self.optimizer.step()
return loss.item()
def valid_step(self, x, y):
with torch.no_grad():
Y = self.model(x, orthonorm_step=False)
if self.siamese_net is not None:
self.siamese_net.eval()
with torch.no_grad():
x = self.siamese_net.forward_once(x)
W = get_affinity_matrix(x, self.dataset).to(self.device)
# if self.counter % 10 == 0:
# plot_laplacian_eigenvectors(Y, y)
loss = self.loss_function(W, Y)
return loss.item()
def train(self, train_loader, valid_loader):
print("Training SpectralNet: ")
epochs = SPECTRAL_HYPERPARAMS[self.dataset]["num_epochs"]
orthonorm = True
for epoch in range(1, epochs + 1):
epoch_loss = 0.0
batches_len = 0.0
for batch_x, _ in train_loader:
batch_x = batch_x.to(device=self.device)
batch_x = batch_x.view(batch_x.size(0), -1)
if orthonorm:
self.ortho_step(batch_x)
else:
loss = self.train_step(batch_x)
epoch_loss += loss
batches_len += 1
orthonorm = not orthonorm
epoch_loss = epoch_loss / batches_len
validation_loss = self.validate(valid_loader)
self.scheduler.step(validation_loss)
current_lr = self.optimizer.param_groups[0]['lr']
if current_lr <= 1e-8: break
print('SpectralNet learning rate = %.7f' % current_lr)
print('Epoch {} of {}, Train Loss: {:.7f} | Validation Loss: {:.7f}'
.format(epoch, epochs, epoch_loss, validation_loss))
torch.save(self.model.state_dict(), f"./networks/weights/mnist_spectral.pth")
print('Finished training SpectralNet')
def validate(self, valid_loader):
validate_loss = 0.0
self.model.eval()
with torch.no_grad():
for batch_x, batch_y in valid_loader:
batch_x = batch_x.to(device=self.device)
batch_x = batch_x.view(batch_x.size(0), -1)
loss = self.valid_step(batch_x, batch_y)
validate_loss += loss
self.counter += 1
validate_loss = validate_loss / len(valid_loader)
return validate_loss
Brief explanation:
The goal of this network is to approximate the eigenvectors of the Laplacian matrix that is obtained from an affinity matrix W.
In the training process, the network samples a batch of data points computes W from the batch, and minimizes the following loss:
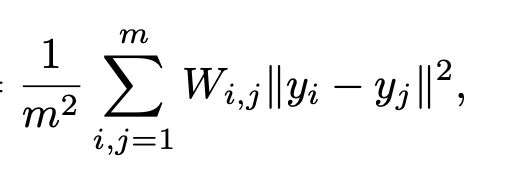
where y_i are the outputs of the network.
There is also an orthogonalization layer (self.orthonorm_weights) that is used the make the output orthogonal.
I would be really happy if you have any idea to what can cause my problem!!