Could anyone explain how this Gumbel-Max pytorch code implementation works ?
Hello,
the standart forumla for the Gumbel - Max is
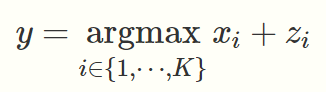
The problem is that argmax is not differentiable.
Your medium source derives this correlation:

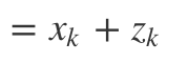
So I would usually use softargmax as a nice approximation for argmax, but this implementation you’ve found does something quite similar.
It basically calculates this formula:
probs = exp{ ((gumbel + log(pi)) / tau) } / sum[j] { exp{ ((gumbel_j + log(pi_j)) / tau) } }
tau is a scaling / temparature parameter where if you decrease it, it will approximate the argmax, and when you increase it the probs will become more uniform.
Last but not least, the max value is taken so that a one - hot - encoding can be made.
(I still find the softargmax nicer as you would matmul the probs with a range tensor (you would choose a relatively small tau (I guess with softargmax it’s called beta and would be chosen high while not being used as a denominator).
Please let me know if there is a performance or other reason why one should do it the way it is done in this implementation.)
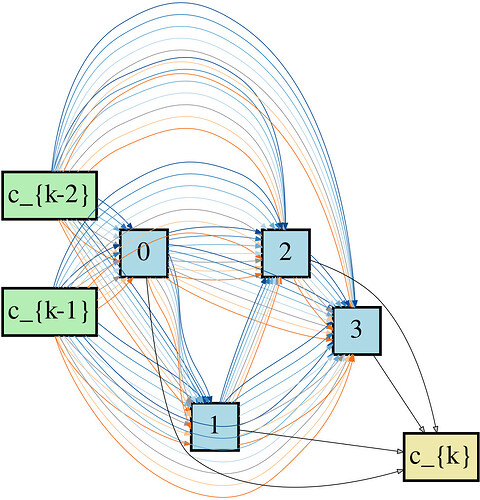
For the NAS multigraph and equation (7) of GDAS paper , how to do backpropagation across multiple parallel edges between two nodes ?