Hello folks.
I create an dqn implement according the tutorial reinforcement_q_learning, with the following changes.
- Use gym observation as state
- Use an MLP instead of the DQN class in the tutorial
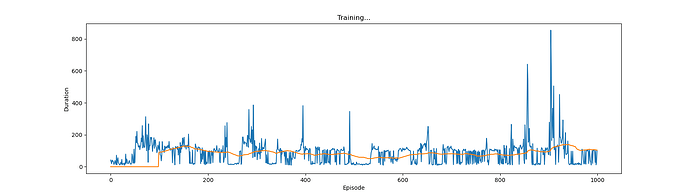
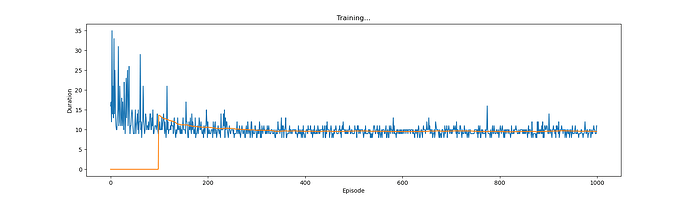
The model diverged if loss = F.smooth_l1_loss{ loss_fn = nn.SmoothL1Loss()} ,
If loss_fn = nn.MSELoss(), the model seems to work (much slower than the tutorial)
What did I do wrong? Any ideas?
import math
import random
import numpy as np
from collections import namedtuple
import matplotlib.pyplot as plt
from itertools import count
from time import sleep
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.autograd import Variable
import gym
use_cuda = False
FloatTensor = torch.cuda.FloatTensor if use_cuda else torch.FloatTensor
LongTensor = torch.cuda.LongTensor if use_cuda else torch.LongTensor
ByteTensor = torch.cuda.ByteTensor if use_cuda else torch.ByteTensor
Tensor = FloatTensor
env = gym.make('CartPole-v0')
Transition = namedtuple('Transition', ('state', 'action', 'next_state', 'reward'))
class ReplayMemory(object):
def __init__(self, capacity):
self.capacity = capacity
self.memory = []
self.position = 0
def push(self, *args):
if len(self.memory) < self.capacity:
self.memory.append(None)
self.memory[self.position] = Transition(*args)
self.position = (self.position + 1) % self.capacity
def sample(self, batch_size):
return random.sample(self.memory, batch_size)
def __len__(self):
return len(self.memory)
BATCH_SIZE = 128
GAMMA = 0.999
EPS_START = 0.9
EPS_END = 0.05
EPS_DECAY = 200
model = nn.Sequential(
nn.Linear(4,1024),
nn.ReLU(),
nn.Linear(1024,1024),
nn.ReLU(),
nn.Linear(1024,2)
)
optimizer = optim.Adam(model.parameters(), lr=1e-4)
loss_fn = nn.MSELoss()
# loss_fn = nn.SmoothL1Loss()
memory = ReplayMemory(10000)
steps_done = 0
def select_action(state):
global steps_done
sample = random.random()
eps_threshold = EPS_END + (EPS_START - EPS_END) * math.exp(-1. * steps_done / EPS_DECAY)
steps_done += 1
if sample > eps_threshold:
output = model(Variable(state.view(-1, 4), volatile=True))
output = output.data
_, index = output.max(1)
print(f'State By Model {output}')
print(f'State By Model {index[0]}')
return index.view(1, 1)
else:
index = random.randrange(2)
# print(f'State By Random {index}')
return LongTensor([[index]])
episode_durations = []
def plot_durations():
plt.figure(2)
plt.clf()
durations_t = torch.FloatTensor(episode_durations)
plt.title('Training...')
plt.xlabel('Episode')
plt.ylabel('Duration')
plt.plot(durations_t.numpy())
# Take 100 episode averages and plot them too
if len(durations_t) >= 100:
means = durations_t.unfold(0, 100, 1).mean(1).view(-1)
means = torch.cat((torch.zeros(99), means))
plt.plot(means.numpy())
plt.pause(0.1) # pause a bit so that plots are updated
last_sync = 0
def optimize_model():
global last_sync
if len(memory) < BATCH_SIZE:
return
transitions = memory.sample(BATCH_SIZE)
# Transpose the batch (see http://stackoverflow.com/a/19343/3343043 for
# detailed explanation).
batch = Transition(*zip(*transitions))
state_batch = [s.view(1,-1) for s in batch.state]
state_batch = torch.cat(state_batch, 0)
state_batch = Variable(state_batch)
action_batch = torch.cat(batch.action)
action_batch = Variable(action_batch)
reward_batch = torch.cat(batch.reward)
reward_batch = Variable(reward_batch)
# Compute Q(s_t, a) - the model computes Q(s_t), then we select the
# columns of actions taken
model_outputs = model(state_batch)
state_action_values = model_outputs.gather(1, action_batch)
non_final_mask = map(lambda s: s is not None, batch.next_state)
non_final_mask = tuple(non_final_mask)
# Compute a mask of non-final states and concatenate the batch elements
non_final_mask = ByteTensor(non_final_mask)
# We don't want to backprop through the expected action values and volatile
# will save us on temporarily changing the model parameters'
# requires_grad to False!
non_final_next_states = [s.view(1, -1) for s in batch.next_state if s is not None]
non_final_next_states = torch.cat(non_final_next_states, 0)
non_final_next_states = Variable(non_final_next_states, volatile=True)
# Compute V(s_{t+1}) for all next states.
next_state_values = Variable(torch.zeros(BATCH_SIZE).type(Tensor))
next_model_outputs = model(non_final_next_states)
max_next_state_values, _ = next_model_outputs.max(1)
next_state_values[non_final_mask] = max_next_state_values
# Now, we don't want to mess up the loss with a volatile flag, so let's
# clear it. After this, we'll just end up with a Variable that has
# requires_grad=False
next_state_values.volatile = False
# Compute the expected Q values
expected_state_action_values = (next_state_values * GAMMA) + reward_batch
# Compute Huber loss
loss = loss_fn(state_action_values, expected_state_action_values)
print(f'Loss={loss.data[0]}');
# Optimize the model
optimizer.zero_grad()
loss.backward()
# for param in model.parameters(): param.grad.data.clamp_(-1, 1)
optimizer.step()
num_episodes = 1000
for i_episode in range(num_episodes):
# Initialize the environment and state
observation = env.reset()
state = FloatTensor(observation)
for t in count():
env.render()
# print(f'State:{state.tolist()}')
action = select_action(state)
step_action = action[0, 0]
observation, reward, done, info = env.step(step_action)
# print(f'observation={observation}')
# print(f'reward={reward}')
# print(f'done={done}')
reward = Tensor([reward])
# Observe new state
next_state = FloatTensor(observation) if not done else None
# Store the transition in memory
assert state is not None
memory.push(state, action, next_state, reward)
# if next_state is not None : print(f'NextState:{next_state.tolist()}')
# Move to the next state
state = next_state
# Perform one step of the optimization (on the target network)
optimize_model()
if done:
episode_durations.append(t + 1)
plot_durations()
break