High order derivatives in loss terms

autograd
1

Hi,
I am implementing high order derivatives for PyTorch. All existing implementation I saw require that the target tensor will be scalar, while my implementation is for any arbitrary tensor.

I developed a functon that for a model (or function) model and input values x, it will return derivatives up to the orderth order, for all x values. When passing a NN, this function must be called at the start of each step\epoch, because it zeros the grads of the optimizer’s params.

def get_high_order_analytic_derivative(model, x, order, optimizer=None):

    result = []

    x_grad = model(x)
    result.append(x_grad)

    while order > 0:
        x.grad = None
        x_grad.backward(torch.ones_like(x), create_graph=True, retain_graph=True)
        x_grad = x.grad
        result.append(x_grad)
        order -= 1

    x.grad = None
    if optimizer is not None:
        optimizer.zero_grad()  # remove trace of calculations from the parameters
    return result

I confirmed the correctness of the function with this example:

a = torch.randn(10, requires_grad=True)
f, df, ddf = get_high_order_analytic_derivate(torch.sin, a, 2)
f
Out[95]: 
tensor([ 0.7344,  0.9864,  0.4804, -0.9276, -0.5895, -0.2465, -0.9672,  0.9168,
         0.3063, -0.6023], grad_fn=<SinBackward>)
df
Out[96]: 
tensor([ 0.6788, -0.1645,  0.8770,  0.3736,  0.8078,  0.9691, -0.2539, -0.3994,
         0.9519,  0.7983], grad_fn=<CopyBackwards>)
ddf
Out[97]: 
tensor([-0.7344, -0.9864, -0.4804,  0.9276,  0.5895,  0.2465,  0.9672, -0.9168,
        -0.3063,  0.6023], grad_fn=<CopyBackwards>)
f + ddf
Out[98]: tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], grad_fn=<AddBackward0>)

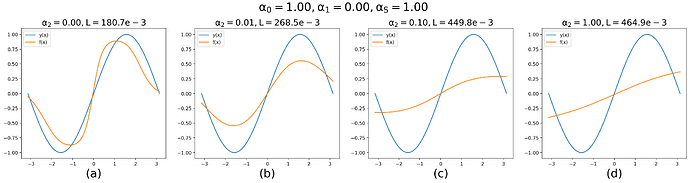
I want a NN to learn the sine function, and one of the loss terms is MSE between (f + ddf) and zeros_like(f + ddf), over some grid of inputs. However, I found that this specific term harms the convergence to my desired model. It think it smoothes my model.

What could be the problem? Is there a problem with using differential equations as loss terms when training NNs? Or maybe my way of calculating the derivatives is not desirable? (notice how I call zero grad so all the calculations shouldn’t change the state of the model)

This is an illustration of adding it as a loss term with growing significance:

for_pytorch
for_pytorch4019×1069 219 KB

The blue line is actual sin and the orange is my model.

2

An unsolicited bit of advice:

don’t do that! Just use x_grad, = torch.autograd.grad(....). It is easy to get a memory leak if you use x.grad in autograd because it uses C++ shared pointers that are not garbage collected and so cycles will wreck havoc.

Edit: The sign here is wrong and so it’s bogus, sorry!

So one thing to say is that for the sine function f = sin(ωx), you have that ddf = ω**2 f, so indeed f + ddf in the loss term is something like (1+ω**2) f and would seem to push f towards 0. It might be better to put the function and ddf into separate terms.

More generally, I think it’s always good to look at each loss terms’s contribution to the loss.

Best regards

Thomas

2 Likes
3

Hi,

There is no issue with using derivatives in loss term. For instance, you can solve Poisson PDE using its equation as loss function (and applying boundary/initial condition).

I think there might be an issue with your model definition or the way you obtain grads.
Siren paper might be able to help you, please see this notebook.

It solves PDEs by including the equation in loss function and/or supervising derivative of ground truth.

As @tom pointed precisely, best way is to use torch.autograd.grad. For instance,

def gradient(y, x, grad_outputs=None):
    if grad_outputs is None:
        grad_outputs = torch.ones_like(y)
    grad = torch.autograd.grad(y, [x], grad_outputs=grad_outputs, create_graph=True)[0]
    return grad

Bests

2 Likes
4

Note that the loss term here seems to have the wrong sign between the terms if the frequency matches…

1 Like
5

Thanks! I updated my code accordingly.
Unfortunately results stay the same.
I get better results with numerical gradients (f’(x) = f(x + d) - f(x - d) / 2d)), but still want to use the analytical if possible, so I’ll keep investigating it.

BTW: ω=1 in my code.

6

ddf is -ω^2 f and not ω^2 f .

And in my case ω = 1, so for learning sin(x), I think MSE(f + ddf, zeros) should be a good loss term

Thanks

1 Like
7

Oh right. I’m so stupid sometimes. Sigh.
PS: Do you have the code somewhere?