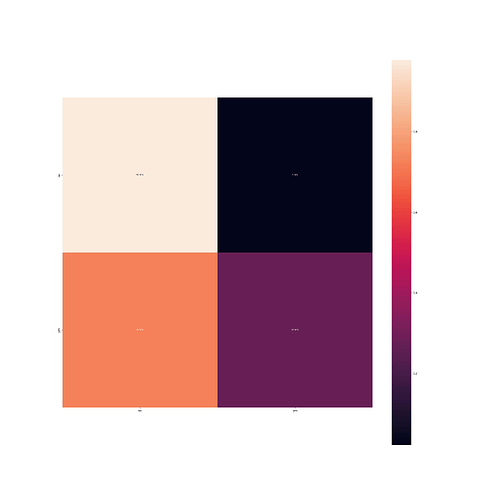High precision and recall but poor confusion matrix

1

I am training a computer vision model with multiple outputs. One of the outputs is a binary class that we will call “has_a_car”.
I am noticing the model has a really high precision and recall (and therefore F-1) on the output “has_a_car”: they are all close to 95%. Question: how is the precision computed? Is it computed on both values (the output is binary) and then the macro average is done? Or it computed only on one of the two classes (i.e. the positive class)? In the latter case, which would be the positive class for PyTorch?
I also noticed that the accuracy is a bit lower, at about 65% and this seems strage. Even stranger, the confusion matrix, is not good at all.

image
image2500×2500 144 KB

Looking at the second row of the confusion matrix, shouldn’t the precision be really bad? The only explanation I could think of is the precision being computed on only one class (not having a car) rather than both.
Here’s how I defined the metrics. The code contains a variable attribute which I am not defining here, but as you can see the same variables are used for every metric:

accuracy_metric = torchmetrics.Accuracy(
    ignore_index=Attribute.ATTRIBUTE_VALUE_NONE.index,
    average='macro',
    num_classes=len(attribute.get_values(include_none=False)),
)
precision_metrics = torchmetrics.Precision(
    ignore_index=Attribute.ATTRIBUTE_VALUE_NONE.index,
    average='macro',
    num_classes=len(attribute.get_values(include_none=False))
)
recall_metrics = torchmetrics.Recall(
    ignore_index=Attribute.ATTRIBUTE_VALUE_NONE.index,
    average='macro',
    num_classes=len(attribute.get_values(include_none=False))
)
f1_metrics = torchmetrics.F1Score(
    ignore_index=Attribute.ATTRIBUTE_VALUE_NONE.index,
    average='macro',
    num_classes=len(attribute.get_values(include_none=False))
)
confusion_matrix_metrics = torchmetrics.ConfusionMatrix(
    num_classes=len(attribute.get_values(include_none=False)),
    ignore_index=Attribute.ATTRIBUTE_VALUE_NONE.index,
    normalize='true',
    nan_strategy='ignore'
)

Does this look correct? Is there any explanation for the precision and confusion matrix being so different? Maybe the normalization in the confusion matrix?
Thank you