Holding a linear layer weight at zero through backpropagation

1

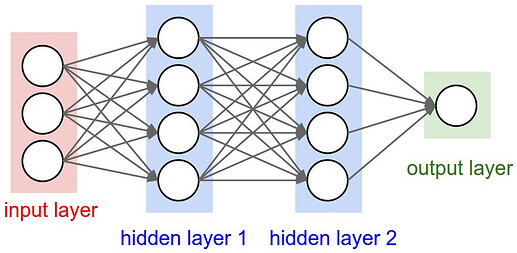
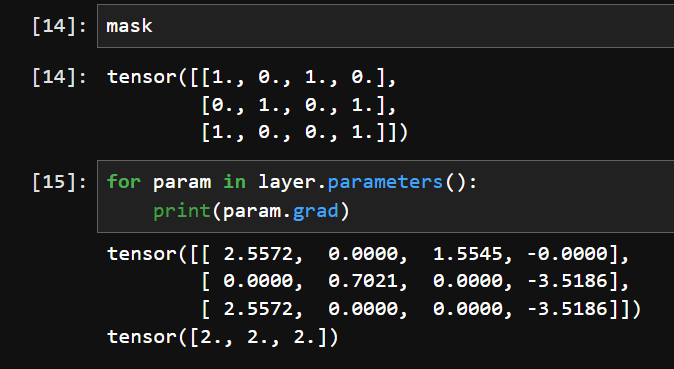
How does one create a permanently partially connected linear layer?

I am trying to create a Linear layer where certain weights are held at zero and skipped during backpropagation so the weight doesn’t change from zero.

In the below image, imagine one of the connecting lines having a permanent weight of zero preventing communication between two neurons or between an input and neuron.

image
image791×388 72.3 KB

I’ve been trying to accomplish this by experimenting at the tensor level by setting
requires_gradient = False
for the scalar tensor at some index of a containing tensor, but I can’t get it to work.

After seeing the error message:
RuntimeError: you can only change requires_grad flags of leaf variables. If you want to use a computed variable in a subgraph that doesn't require differentiation use var_no_grad = var.detach().

I’ve tried detaching the scalar tensor and re-attaching it to the containing tensor, but requires_grad changes to True when the detached tensor is reattached and I end up right where I started.

Is there any way to hold a linear layer weight at zero through backpropagation? (i.e. backpropagation does not propagate through the connection - as if it were not there.)

2

To ensure that gradients are zero for weights that are permanently set to zero during backpropagation, you can use a masking technique. This will prevent any updates to those weights during the optimization process.

Implementing Zero Gradients for Permanently Zero Weights

Example

import torch
import torch.nn as nn
import torch.nn.functional as F
import math

class MaskedLinear(nn.Module):
    def __init__(self, in_features, out_features, mask):
        super(MaskedLinear, self).__init__()
        self.in_features = in_features
        self.out_features = out_features
        self.weight = nn.Parameter(torch.Tensor(out_features, in_features))
        self.bias = nn.Parameter(torch.Tensor(out_features))
        self.mask = mask  # Binary mask to control connectivity
        self.reset_parameters()

    def reset_parameters(self):
        nn.init.kaiming_uniform_(self.weight, a=math.sqrt(5))
        fan_in, _ = nn.init._calculate_fan_in_and_fan_out(self.weight)
        bound = 1 / math.sqrt(fan_in)
        nn.init.uniform_(self.bias, -bound, bound)

    def forward(self, input):
        return F.linear(input, self.weight * self.mask, self.bias)


in_features = 4
out_features = 3
mask = torch.tensor([[1, 0, 1, 0], [0, 1, 0, 1], [1, 0, 0, 1]], dtype=torch.float32)

layer = MaskedLinear(in_features, out_features, mask)
input_data = torch.randn(2, in_features)
output = layer(input_data).sum()

output.backward()

Output results

{A1F3FBDB-B37E-4172-AA8E-A30F13A77BCA}

I still did not understand why you want to set some specific parameters to zero

1 Like
3

Awesome, thanks so much! Really appreciate it. I think this should allow me to accomplish what I’m trying to do; I’m going to implement it soon.

As to why - I’m experimenting with a novel network architecture, and hopefully this will allow faster processing than the method I’m currently using to accomplish my particular network connections.

1 Like
4

Is it a workaround to set some of the weights as non-trainable?

5

I suppose, yes. That’s another way to put it.

Is there a better way? (i.e. faster processing than the solution provided)

6

So that MaskedLinear class allowed me to do exactly what I wanted. The only problem is that it’s quite slow. It doesn’t matter much anymore for what I’m doing though, as I discovered another shortcoming using this approach for my endeavors.

Here’s the class streamlined using nn.Linear inheritance:

from torch import Tensor, no_grad
from torch.nn import Linear
import torch.nn.functional as F

class MaskedLinear(Linear):
    """ Linear layer that allows for masking of weights preventing
    backpropagation through masked network connections. Masked
    weights initialized to zero.

    Uses a binary mask. i.e. -
    mask = torch.tensor([
        [0, 1, 1, 1],
        [0, 1, 1, 1],
        [0, 1, 1, 1],
        ],
        dtype=torch.float32)
    """

    def __init__(self, in_features: int, out_features: int, mask: Tensor,
                 bias: bool = True, device=None, dtype=None) -> None:
        super().__init__(in_features, out_features, bias, device, dtype)
        self.mask = mask
        with no_grad():
            self.weight *= self.mask

    def forward(self, input: Tensor) -> Tensor:
        return F.linear(input, self.weight * self.mask, self.bias)

It would be nice if there were a way to make this type of thing happen without it being so slow. Theoretically, it seems like it should be possible.

If half the weights in a linear layer were zero and masked, that would mean half as many calculations in the forward pass (well half as many not-trivial calculations anyway) and half the backpropagation. If such a layer could be as fast as a non-masked layer of the same size that’d be good. Currently, with the MaskedLinear it’s slower.

It’s the self.weight * self.mask that makes it slow. If one could just set require_gradient to false for the masked weights instead, I assume it would be faster.