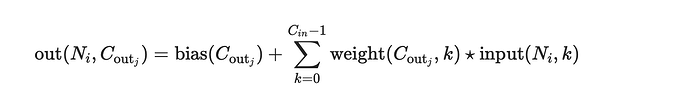How can I come up with a "do nothing" kernel for a Conv1d?

1

I have:

        print('\ninp', inp.min(), inp.mean(), inp.max())
        print(inp)
        out = self.conv1(inp)
        print('\nout1', out.min(), out.mean(), out.max())
        print(out)
        quit()

My min, mean and max for my inp is: inp tensor(9.0060e-05) tensor(0.1357) tensor(2.4454)

For my output, I have: out1 tensor(4.8751, grad_fn=<MinBackward1>) tensor(21.8416, grad_fn=<MeanBackward0>) tensor(54.9332, grad_fn=<MaxBackward1>)

My self.conv1 is:

        self.conv1 = torch.nn.Conv1d(
            in_channels=161,
            out_channels=161,
            kernel_size=11,
            stride=1,
            padding=5)
        self.conv1.weight.data = torch.zeros(self.conv1.weight.data.size())
        self.conv1.weight.data[:, :, 5] = 1.0
        self.conv1.bias.data = torch.zeros(self.conv1.bias.data.size())

So my weights look like: tensor([0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0.])

So if I understand how convolution works, this should produce the same output. But it doesn’t.

What am I doing wrong? I realize that there’s some summing going on, but then how would I have an identity kernel?

2

Note that each kernel has the same number of channels as your input activation, which will be part of the summation, so you would need a depthwise convolution, where each filter acts on a single input channel.

3

How would I do a depthwise convolution in my case?

4

Also - is there any advantage to doing a “depth wise separable convolution”? It seems then the contextual information from the other channels won’t be factored in.

5

Also, I just tried:

        self.conv1 = torch.nn.Conv1d(
            in_channels=feature_dim,
            out_channels= feature_dim,
            kernel_size=kernel_sizes[0],
            stride=1,
            groups= feature_dim,
            padding=kernel_sizes[0] // 2)

This still doesn’t quite get it:

inp tensor(3.2217e-05) tensor(0.1359) tensor(1.9529) torch.Size([1, 161, 32])

out1 tensor(2.0011e-07, grad_fn=<MinBackward1>) tensor(0.0008, grad_fn=<MeanBackward0>) tensor(0.0121, grad_fn=<MaxBackward1>) torch.Size([1, 161, 32])
6

I guess I’m not fully understanding this.

If my input is 10 steps of 161-dimension each, then in the equation:

image
image1360×194 8.77 KB

What is input(Ni, k)?

7

I can’t give you a general answer, as the advantages/disadvantages will depend on your actual use case.
For your use case to get the identical output, you would need to use a depthwise convolution, otherwise the input channels will be summed.

You are most likely getting a different result due to the bias.
Here is an example yielding the same result:

conv = nn.Conv1d(5, 5, kernel_size=11, stride=1, padding=5, groups=5, bias=False)
with torch.no_grad():
    conv.weight.zero_()
    conv.weight[:, :, 5] = 1.

x = torch.randn(2, 5, 24)
out = conv(x)
print((out == x).all())
> tensor(True)

N_i is used to index the batch dimension, while k is used to index the input channel dimension.

Have a look at CS231n - Convolution for a detailed description about the shape and workflow of convolutions. While the post is focused on 2D convolutions, the general method also applies for 1D convs.