A balanced dataset allows us to detect overfitting or under fitting by comparing train and validation error. But is this comparison meaningful for imbalanced dataset when we use class-weight in binary cross entropy loss calculation?
How we can find the best model?
Weighting a loss allows you to use the actual loss value as a proxy for the metric you care about.
E.g. assume you are dealing with an imbalanced dataset containing 99% class0 and only 1% class1 samples. If your model does not learn the underling distribution but only returns class0 as the predicted class, the loss would have a low value and the accuracy would already be at 99%, which might look great but it quite useless. This case is also known as the Accuracy paradox.
To avoid this, you would try to force the model to learn the actual class distribution by using a weighted loss and might want to check another metric (e.g. the F1-score instead of the accuracy). The loss still acts as a proxy for your metric, so I would assume you would also use it during the validation phase.
Let’s see if other users have other opinions about it.
Hi Maryam!
Yes, provided that what you call your “error” is the loss criterion you use
for training (in your case weighted binary cross entropy), or, if your error
is not your actual training loss, then at least – to use @ptrblck’s language –
your loss is a good “proxy for the metric you care about.”
The short story is that provided your training and validation datasets are
similar in character and you use the same loss criterion for both, including
class weights, if you have them, then divergence between your validation
and training losses indicates overfitting.
In a narrow technical sense you can still talk about overfitting even if your
training loss isn’t a good match for the “metric you care about” (although in
such a case you won’t be training your model to do what you really want
it to do) – it’s still logically consistent to say that you are overfitting your
training set with respect to the loss criterion you are training with.
What matters is that your training and validation data sets have the same
character and, in the case of unbalanced data, have the same relative
class weights. The cleanest way to do this – if you can, which you generally
should be able to – is to have your training and validation data sets come
from the same larger data set.
Let’s say you have 10,000 individual data samples. If you randomly split
this data set into a training set of, say, 8,000 samples and a validation set
of 2,000 samples, the two datasets will be statistically identical. In particular,
they will have (statistically*) the same relative class weights,
Train your training set with a loss criterion of weighted binary cross entropy
and also track the same weighted binary cross entropy on your validation
set. If your validation-set loss starts going up, even as your training-set loss
keeps going down, overfitting has set in, and further training is actually
making your model worse, rather than better. (Note, if the “metric you care
about” doesn’t track your training loss, then your model may or may not
perform well on the “metric you care about,” but that’s a separate issue
from overfitting.)
*) Let’s say that your whole dataset of 10,000 contains 1% positive
samples – that is 100 positive samples – and you randomly split it 80/20.
Then your validation set of 2,000 samples will contain about 20 positive
samples. But this number could easily range from something like 15 to
25 positive samples, which could be enough of a difference to somewhat
affect your validation-loss computation. If you want to be fancier, you
could separately randomly split your positive and negative samples 80/20
so that your validation set contains exactly 20 positive samples (and your
training set, 80). The smaller your dataset and the greater your class
imbalance, the more this nuance will matter.)
Best.
K. Frank
The plot shows the loss function values. Which epoch shows the best model or, in other words, when should I stop learning?
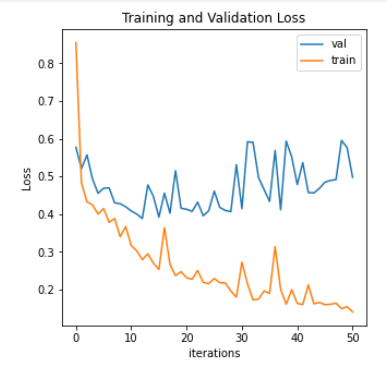
Hi Maryam!
Your loss plot is somewhat noisy, so it’s a bit of a judgment call. To my eye
I would say:
It looks to me that your training loss is going down systematically throughout
your entire plot. Your validation loss appears to be going down up to about
iteration 12. Mentally trying to average some of the noise away, I would say
that your validation starts drifting up after iteration 12, but you could argue
that there’s a plateau from iteration 12 up to about iteration 25 or 30. Your
“best” model almost certainly occurs between iterations 12 and 30.
A legitimate rule of thumb for picking a good candidate for your best model
is to choose the model with the lowest validation loss – in your case
seemingly that at iteration 12. This won’t necessarily be your best model,
but based just on the information in your loss plot, it’s probably the best
choice you can make.
Having said that, depending on the complexity of your model (and the size
of your training set), 50 epochs of training is not a lot. If you can afford the
training time, it would be prudent to continue training significantly longer,
perhaps for thousands of epochs. In all probability, your training loss will
continue to trend down and then flatten out, while your validation loss
continues to increase as you continue to overfit. But it’s possible that your
training is temporarily “stuck” and as you continue training it will find a better
“direction” to explore, causing your validation loss to start going down again.
(Also try experimenting with your training hyperparameters, such as learning
rate and momentum, and your choice of optimizer.)
Best.
K. Frank
Frank already said a rule of thumb. But, for some common cases (e.g. Cifar 10-100 dataset), validation error (accuracy error, not loss) can keep decreasing even though validation loss start decreasing after some point. So, if your measure of performance is based on accuracy and validation error keeps decreasing (which it probably is), you might keep training until 30 epoch in your case.
There was even a theoretical framework to understand this behaviour called IB (Information Bottleneck) Principle, which was later disputed to be invalid e.g. in presence of ReLU activation
One thing to certainly emphasize: choose your validation metric carefully and based on your goal.
Thanks for your detailed responses.
Sorry, but I need two more tips from you:
I should report the average results under multiple runs and their standard deviation,so I need a metric to get the best model in per execution.
- The best model (iteration) in several papers I read about this dataset is the one with the highest AUC, without considering train/validation loss. Could it be true in machine learning concepts?
- The second challenge is that I believe AUC is not enough to find the best model, and we also need macro F1 and G-mean. Is it possible to combine them to get the best model. As an example, set a threshold for the F1-score and the G-mean, then the best model is the one with the highest AUC and a higher value than the thresholds for the F1-score and the G-mean? Can I apply it?
Best Regards,
Maryam
Hi Maryam!
It would be reasonable to use AUC to select your “best” model. The idea
would be that AUC is “the metric you care about” and that binary cross
entropy is the proxy for that metric that you use for training.
Again, this would also be reasonable. Now you would be using some
combination of AUC, F1, and G-mean as “the metric you care about”
and using it to select your “best” model.
In either case, I would probably still use a divergence between binary
cross entropy as computed for your training and validation sets as an
indication that overfitting has set in (implying that further training will
likely not be helpful). But you can use the divergence between other
metrics as an indication of overfitting.
Note, if you use some metric computed for your validation set to stop
training (because of overfittiing) and especially if you use some metric
computed for your validation set to select your “best” model, you should
not use your validation set to report final performance numbers. Instead
you should use a separate “test set.” In a common approach, your would
take your entire dataset and randomly split it into three sets – a training
set for training, a validation set to monitor overfitting and possibly select
your “best” model, and an entirely separate test set that you don’t look at
during the training and model selection process, but use solely to compute
your final performance metrics.
Best.
K. Frank
Thank you very much. It was very helpful.
How did you end up mixing all those metrics (AUC, F1, and G-mean)