How does SGD weight_decay work?

BrightLamp · December 26, 2018, 4:07pm

Hello,
i write a toy code to check SGD weight_decay.
but it seems to have no effect to the gradient update.
am i misunderstand the meaning of weight_decay?
thank you very much.

PyTorch 1.0

import torch
import numpy as np

np.random.seed(123)
np.set_printoptions(8, suppress=True)

x_numpy = np.random.random((3, 4)).astype(np.double)
w_numpy = np.random.random((4, 5)).astype(np.double)
x_torch = torch.tensor(x_numpy, requires_grad=True)
w_torch = torch.tensor(w_numpy, requires_grad=True)

lr = 0.1
sgd = torch.optim.SGD([w_torch], lr=lr, weight_decay=0.9)

y_torch = torch.matmul(x_torch, w_torch)
loss = y_torch.sum()

print("w_torch before SGD")
print(w_torch.data.numpy())

sgd.zero_grad()
loss.backward()
sgd.step()

w_grad = w_torch.grad.data.numpy()

print("w_torch after SGD")
print(w_torch.data.numpy())

print("check_weight_decay")
print(w_numpy - lr * w_grad)

"""
code output :

w_torch before SGD
[[ 0.43857224  0.0596779   0.39804426  0.73799541  0.18249173]
 [ 0.17545176  0.53155137  0.53182759  0.63440096  0.84943179]
 [ 0.72445532  0.61102351  0.72244338  0.32295891  0.36178866]
 [ 0.22826323  0.29371405  0.63097612  0.09210494  0.43370117]]
w_torch after SGD
[[ 0.20941374 -0.13538012  0.17253327  0.48188881 -0.02361953]
 [ 0.04952477  0.37357542  0.37382677  0.46716854  0.6628466 ]
 [ 0.50417498  0.40095203  0.50234411  0.13881324  0.17414831]
 [ 0.01120012  0.07076036  0.37766885 -0.11270393  0.19814865]]
check_weight_decay
[[ 0.20941374 -0.13538012  0.17253327  0.48188881 -0.02361953]
 [ 0.04952477  0.37357542  0.37382677  0.46716854  0.6628466 ]
 [ 0.50417498  0.40095203  0.50234411  0.13881324  0.17414831]
 [ 0.01120012  0.07076036  0.37766885 -0.11270393  0.19814865]]
"""

rasbt · December 26, 2018, 4:27pm

The weight_decay parameter adds a L2 penalty to the cost which can effectively lead to to smaller model weights. It seems to work in my case:

import torch
import numpy as np

np.random.seed(123)
np.set_printoptions(8, suppress=True)

x_numpy = np.random.random((3, 4)).astype(np.double)
w_numpy = np.random.random((4, 5)).astype(np.double)
x_torch = torch.tensor(x_numpy, requires_grad=True)
w_torch = torch.tensor(w_numpy, requires_grad=True)

#######################################################

print('Original weights', w_torch)

lr = 0.1
sgd = torch.optim.SGD([w_torch], lr=lr, weight_decay=0)

y_torch = torch.matmul(x_torch, w_torch)
loss = y_torch.sum()

sgd.zero_grad()
loss.backward()
sgd.step()

w_grad = w_torch.grad.data.numpy()
print('0 weight decay', w_torch)


#######################################################

w_torch = torch.tensor(w_numpy, requires_grad=True)

print('Reset Original weights', w_torch)

sgd = torch.optim.SGD([w_torch], lr=lr, weight_decay=1)

y_torch = torch.matmul(x_torch, w_torch)
loss = y_torch.sum()

sgd.zero_grad()
loss.backward()
sgd.step()

w_grad = w_torch.grad.data.numpy()
print('1 weight decay', w_torch)

This returns

Original weights tensor([[0.4386, 0.0597, 0.3980, 0.7380, 0.1825],
        [0.1755, 0.5316, 0.5318, 0.6344, 0.8494],
        [0.7245, 0.6110, 0.7224, 0.3230, 0.3618],
        [0.2283, 0.2937, 0.6310, 0.0921, 0.4337]],
       dtype=torch.float64, requires_grad=True)
0 weight decay tensor([[ 0.2489, -0.1300,  0.2084,  0.5483, -0.0072],
        [ 0.0653,  0.4214,  0.4217,  0.5243,  0.7393],
        [ 0.5694,  0.4559,  0.5674,  0.1679,  0.2067],
        [ 0.0317,  0.0972,  0.4345, -0.1044,  0.2372]],
       dtype=torch.float64, requires_grad=True)
Reset Original weights tensor([[0.4386, 0.0597, 0.3980, 0.7380, 0.1825],
        [0.1755, 0.5316, 0.5318, 0.6344, 0.8494],
        [0.7245, 0.6110, 0.7224, 0.3230, 0.3618],
        [0.2283, 0.2937, 0.6310, 0.0921, 0.4337]],
       dtype=torch.float64, requires_grad=True)
1 weight decay tensor([[ 0.2050, -0.1360,  0.1686,  0.4745, -0.0254],
        [ 0.0478,  0.3683,  0.3685,  0.4608,  0.6544],
        [ 0.4969,  0.3948,  0.4951,  0.1356,  0.1705],
        [ 0.0089,  0.0678,  0.3714, -0.1136,  0.1938]],
       dtype=torch.float64, requires_grad=True)

As you can see, the weights are smaller when I use weight_decay=1 compared to weight_decay=0

BrightLamp · December 26, 2018, 6:55pm

Hello, rasbt

here is another check code :

import torch
import numpy as np

np.random.seed(123)
np.set_printoptions(8, suppress=True)

x_numpy = np.random.random((3, 4)).astype(np.double)
x_torch = torch.tensor(x_numpy, requires_grad=True)
x_torch2 = torch.tensor(x_numpy, requires_grad=True)

w_numpy = np.random.random((4, 5)).astype(np.double)
w_torch = torch.tensor(w_numpy, requires_grad=True)
w_torch2 = torch.tensor(w_numpy, requires_grad=True)

lr = 0.1
weight_decay = 0.9
sgd = torch.optim.SGD([w_torch], lr=lr, weight_decay=0)
sgd2 = torch.optim.SGD([w_torch2], lr=lr, weight_decay=weight_decay)

y_torch = torch.matmul(x_torch, w_torch)
y_torch2 = torch.matmul(x_torch2, w_torch2)

loss = y_torch.sum()
loss2 = y_torch2.sum()

sgd.zero_grad()
sgd2.zero_grad()

loss.backward()
loss2.backward()

sgd.step()
sgd2.step()

w_grad = w_torch.grad.data.numpy()
w_grad2 = w_torch2.grad.data.numpy()

print("check_grad")
print(w_grad + weight_decay * w_numpy)
print(w_grad2)

"""
check_grad
[[ 2.29158508  1.95058016  2.25510989  2.56106592  2.06111261]
 [ 1.25926989  1.57975955  1.58000814  1.67232418  1.86585193]
 [ 2.20280346  2.10071483  2.20099271  1.84145669  1.87640346]
 [ 2.17063112  2.22953686  2.53307273  2.04808866  2.35552527]]
[[ 2.29158508  1.95058016  2.25510989  2.56106592  2.06111261]
 [ 1.25926989  1.57975955  1.58000814  1.67232418  1.86585193]
 [ 2.20280346  2.10071483  2.20099271  1.84145669  1.87640346]
 [ 2.17063112  2.22953686  2.53307273  2.04808866  2.35552527]]
 """

rasbt · December 26, 2018, 7:21pm

The part that I circled doesn’t seem right to me:

In L2 regularization, you modify the cost as follows

The weight update should be then

The way PyTorch applied the weight decay seems correct to me (you can drop the factor 2)

InnovArul · December 26, 2018, 10:11pm

If you look closely, the formula that you circled is just a rearrangement of the usual SGD weight decay formula I guess.

rasbt · December 26, 2018, 10:31pm

Ooops, you are right, they are exactly the same.

Dhorka · May 30, 2019, 9:04am

I have a doubt here. In pytorch the weigh decay, is it only applied to the weighs or to all the parameters that requires gradient? I mean for instance if I use this piece of code:

optimizer = torch.optim.Adam(model.parameters(), lr=args.lr, betas=args.betas, weight_decay=args.wd)

Will be the weight decay applied to all the parameters of the model including bias and batchnorm parameters?

Thanks

bintonto · May 30, 2019, 1:27pm

   def step(self, closure=None):
        """Performs a single optimization step.

        Arguments:
            closure (callable, optional): A closure that reevaluates the model
                and returns the loss.
        """
        loss = None
        if closure is not None:
            loss = closure()

        for group in self.param_groups:
            weight_decay = group['weight_decay']
            momentum = group['momentum']
            dampening = group['dampening']
            nesterov = group['nesterov']

            for p in group['params']:
                if p.grad is None:
                    continue
                d_p = p.grad.data
                if weight_decay != 0:
                    d_p.add_(weight_decay, p.data)
                if momentum != 0:
                    param_state = self.state[p]
                    if 'momentum_buffer' not in param_state:
                        buf = param_state['momentum_buffer'] = torch.clone(d_p).detach()
                    else:
                        buf = param_state['momentum_buffer']
                        buf.mul_(momentum).add_(1 - dampening, d_p)
                    if nesterov:
                        d_p = d_p.add(momentum, buf)
                    else:
                        d_p = buf

                p.data.add_(-group['lr'], d_p)

        return loss

 d_p = p.grad.data
 if weight_decay != 0:
     d_p.add_(weight_decay, p.data)

so… weight_decay * w is already included in w_grad

Dhorka · May 30, 2019, 4:18pm

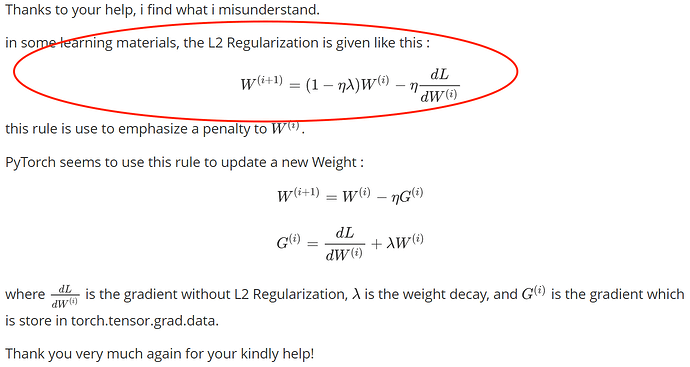
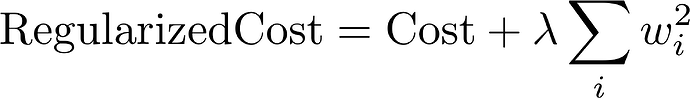
Thanks for your reply but it is not answering my question . I will try to explain better. My concern is to know if the weigh_decay functionality is able to distinguish between weighs, bias and learning parameters of batchnorm. Because, Normally weight decay is only applied to the weights and not to the bias and batchnorm parameters (do not make sense to apply a weight decay to the batchnorm parameters). For this reason I am asking if the weigh decay is able to distinguish between this kind of parameters. My feelings after see the code is that weight_decay functionality is not able to distinguis between these parameters, but I would like to have the confirmation.

Konstantin_Burlachen · December 17, 2021, 12:48am

So let me summarize.
From experiments and from F.sgd code we may observe that weight_decay is in fact add $\ambda w_i$

So:

Original modified code
"print(w_numpy - lr * (w_grad+0.9*w_numpy))"
produce the same result as
"print(w_torch.data.numpy())"
Error in the question was in ignoring the weight_decay parameter.
"The weight_decay parameter adds an L2 penalty to the cost". Such a response is too vague, such a thing as the L2 penalty does not exist in mathematics.

Please don’t blame me, but you use several words from math:

L2 is a name from math that stands for the norm. And it’s not true that you use the L2 norm at all. What you use is the L2 norm square of all vectors of parameters. It’s not L2 norm.
You use the word “Penalty” penalty can be as a constraint or extra term in objective. If it is an extra term then different technics for scalarization are existed.

Next to such responses like “L2 penalty” lead to real problems.

First of all - you multiply it by “\lambda/2”, not by “\lambda”
It’s why such responses add “L2” penalty is too vague, and it only brings too much confusion. It’s better to say everything exactly.

The formula with “2 \lambda” is incorrect as well. And bring only confusion.

So what is implemented in PyTorch is weight_decay corresponds to implicit additive term in the objective function with form $(\lambda/2) |parameters|_2^2$.

dhruvbird · April 26, 2023, 9:08pm

Weight decaying is applied to all the learnable/trainable parameters of the model. If you want to explicitly exclude some parameters from being weight decayed, you will need to do that manually. See the code for configure_optimizers at https://github.com/karpathy/nanoGPT/blob/master/model.py#L270 for an example.

Miro_Mlynarik · May 30, 2023, 5:45pm

Batchnorm parameters are not learnable parameters. They are registered as buffer.

ptrblck · May 30, 2023, 6:01pm

That’s not correct since BatchNorm layers use trainable affine parameters and buffers collecting the running stats as seen here:

bn = nn.BatchNorm2d(3)
print(dict(bn.named_parameters()))
# {'weight': Parameter containing:
# tensor([1., 1., 1.], requires_grad=True), 'bias': Parameter containing:
# tensor([0., 0., 0.], requires_grad=True)}
print(dict(bn.named_buffers()))
# {'running_mean': tensor([0., 0., 0.]), 'running_var': tensor([1., 1., 1.]), 'num_batches_tracked': tensor(0)}