How can I perceive the autograd grad which has been made by pytorch?
Here I have a sample. I do not understand what arrows are or what AccumulatedGrads are and how I can interpret this graph?
Here is the actual function:
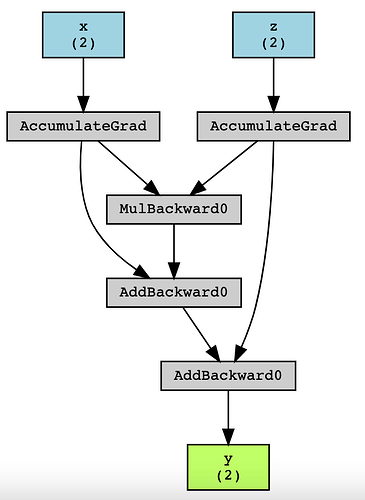
y = x*z + x + z
Hi Mahdi!
The arrows indicate the direction of the forward pass. Note, that the terms
“root” and “leaves” of the graph correspond to the backward pass starting
at the root and ending at the leaves.
The two top (blue) boxes are the two leaves, and indicate that x and z
have shape [2].
“AccumulateGrad” is a special-purpose “grad_fn” that indicates that the
backward pass should accumulate the computed gradient into the .grad
of the leaf tensor.
Python parses expressions with multiplication (*) taking precedence over
addition (+), and with operators of equal precedence parsed left to right.
So (in the forward pass that builds the graph), first you get two arrows
linking x and z to “MulBackward0”. This is the * in the expression.
Then you get two arrows linking the result of the “MulBackward0” box
(namely x*z) and x itself to an “AddBackward0”. This is the first + in
the expression, reading left to right.
Then you get two arrows linking the first “AddBackward0” box (namely
x*z + x) and z to a second “AddBackward0”. This is the second +.
The result of the second “AddBackward0” box is the whole expression,
x*z + x + z, and is linked by an arrow to the bottom (green) box – the
root – that indicates that y is also a tensor of shape [2].
Best.
K. Frank
Thanks,
I saw that there are two arrows from AccumulatedGrad to AddBackward0s, so may I know what they point to?
Which two arrows from AccumulatedGrad to AddBackward0s are you referring to?
There is one direct arrow from x (AccumulatedGrad) to the first AddBackward0. Similarly, one direct arrow from z (AccumulatedGrad) to the second AddBackward0.
Are you pondering why there are two AddBackward0s in the graph? - It is because xz ‘+’ x is the first addition operation, while xz + x ‘+’ z is the second addition op.
Anything else you were referring to?
Actually no,
There are two AccumulatedGrad in the graph and each has an arrow to any AddBackward. Why the graph pointed from AccumulatedGrad to AddBackward nodes?
Thanks
Each tensor requiring gradients (required_grad=True) is associated with a special grad_fn called AccumulatedGrad which is where the calculated gradients are stored (accumulated) after a backward call.
Why the graph pointed from AccumulatedGrad to AddBackward nodes?
The two AccumulatedGrad are associated with the tensors x and z. The first arrow from x’s AccumulatedGrad to the first AddBackward0 indicates x getting added to xz (the arrow coming from MulBackward0).
The 2nd arrow from z’s AccumulatedGrad to the second AddBackward0 indicates z getting added to xz + x (the arrow coming from the 1st AddBackward0).
Hope that helped.
Srishti