Suppose we have following system:
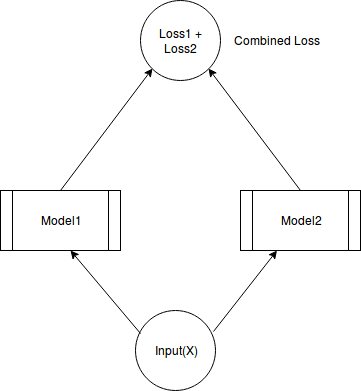
We keep the weights of both the models constant and find out gradient of combined loss with respect to input X.
Now, how the gradient will be calculated for X, given that we have two routes to reach X?
If your loss is L=L1+L2 then the gradients at the input will sum. Consider:
L1=f1(x)
L2=f2(x)
L=f1(x)+f2(x)
The derivative w.r.t x will be the derivative through f1 + the derivative through f2. This is because the derivative of a sum is the sum of the derivatives. If your combined loss is:
L=f1(x)*f2(x)
Then apply the chain rule and you will obtain something similar. And so on.
Hope it helps!
1 Like
So, when combined loss = loss1 + loss2, it is similar to something like following:
optimizer.zero_grad()
loss1.backward(retain_graph=True)
loss2.backward()
optimizer.step()
Am I right?
Yes it is! But Iād recommend you to stick to the first way, because retain_graph can easily lead to errors due to memory consumption etc.
1 Like
exactly, you save memory if you do it directly instead of calling backward two times.