How to build a network consisting of several parallelly connected subnetworks

1

Hi, all,

Recently, I want to use PyTorch to build a slightly special network with the following structure:

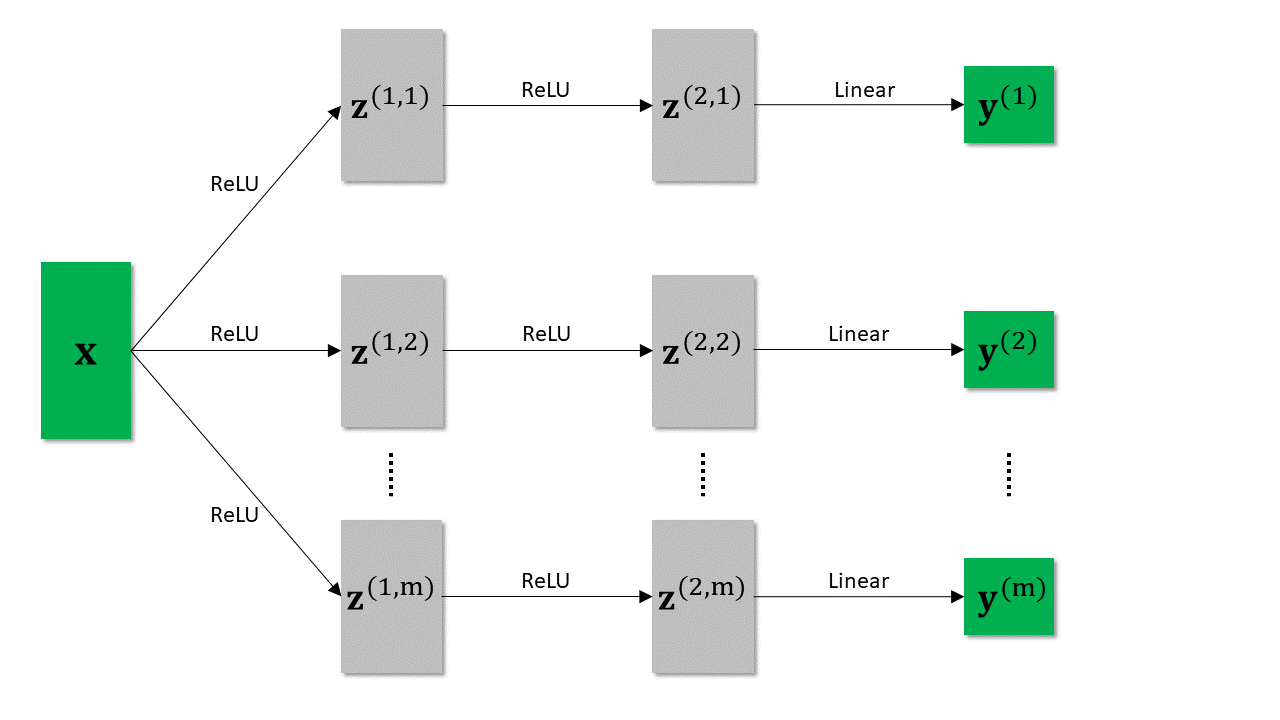
network_structure
network_structure1280×720 27.6 KB

In the above network, the green boxes correspond to known variables, i.e., input vector x and m label vectors y^(1), …, y^(m). Here each y^(i) is a one-hot vector with value (1,0) or (0,1). And the remaining gray boxes indicate hidden representations (e.g., z^(1,1) and z^(2,m)).

My question is for a given positive integer m>1, how to implement such a network in nn.Module class? I guess maybe I need to use nn.ModuleList() and the for loop.

Could anyone please give a further suggestion or comment? Thanks in advance.

1 Like
2

P.S.: all hidden representations in the same layer have the same size, e.g., z^(1,i).size()=(100,1) and z^(2,j).size()=(10,1) for all i and j.

3

A naive approach would indeed be to construct m using nn.ModuleList() and a for loop.
But I think we parallelise the whole lot. The following idea should work, but I haven’t checked all the details.

The input x is shared by all subnetworks, so a single Linear layer of size m*100 followed by separating the result into m parts will work identically to m separate Linear layers of size 100.

self.x_to_z1 = nn.Sequential(
    nn.Linear(x_size, 100*m),
    nn.ReLU(),
)

In forward() we could follow this by .view(batch_size, m, 100) to separate the z^(1,i). Or we could use .view(batch_size, 100, 1) to add a spatial dimension of size 1, and follow up with a grouped convolution.

self.z1_to_z2 = nn.Sequential(
    nn.Conv1d(100*m, 10*m, kernel_size=1, groups=m),
    # the input is grouped into groups of 100 channels, 
    # and each group is used to produce 10 channels of output
    nn.ReLU(),
)

And then another grouped convolution to produce the required number of outputs, i.e. 2 per y^i, if I have understood correctly.

self.z2_to_y = nn.Conv1d(10*m, 2*m, kernel_size=1, groups=m)

And finally you could use .view(batch_size, m, 2) followed by .split(1, dim=1) to split the output into a list of m tensors of size 2. But I suspect you could parallelise the loss function too.

2 Likes
4

Dear @jpeg729,

Thank you so much for your suggestion. I think that your ideas of grouping hidden representations and using 1D convolution are pretty brilliant!!! And I will have a try accordingly.:grin:

Regards,
Zengjie Song

1 Like
5

I have to admit that I would have probably gone for the naive approach, but I took the question as a challenge and had that idea.

One detail that I am not sure of is how the grouped conv groups the channels. Does a Conv1d(100*m, 10*m, 1, groups=m) use the first 100 channels input to produce the first 10 channels output? Or do the first m channels of input & output all belong to different groups? I suspect the former, but I don’t know.

6

Maybe all of these queries would be solved by doing some experiments. I would like to have a try first, and then give the validation results and discoveries. Thanks.

7

Sorry for the delayed reply. After doing some experiments, I found that the alternative method proposed by @jpeg729 is feasible.

8

Hello,

I was looking for clarification on this topic, as I think I am trying the same thing.

The goal here was to construct 3 networks, that all used the same input data, had the same hidden layer structure, but had 3 different outputs correct?

Thank you

9

Yes, that is almost the case discussed here.

Conceptually we expect to obtain a network consisting of 3 (or m) sub-networks that have the same architecture but with different connection weights.

10

Did you find that there were issues with overtraining the network? For example, say that y1 was very easy to learn, but y3 was hard to learn. Was there a single loss function being minimized, or was there a separate loss function for each subnetwork?

If there was a single loss function, I worry then that y1 being easy to learn would result in it being overtrained, due to the difficulty in learning y3.

11

I think that whether overtraining happens depends on many factors, e.g., network architecture, loss function, data, etc.

To address the case that y1 is easy to learn compared with others, maybe we can construct a shared network backbone, and then adding specific head (or sub-network) for each yi. So each sub-network would be learnt separately according to the loss part containing yi.