How to compute Jacobian matrix in PyTorch?

autograd
1

For one of my tasks, I am required to compute a forward derivative of output (not loss function) w.r.t given input X. Mathematically, It would look like this:Screenshot%20(199)
Which is essential a Jacobian of the output. It is different from backpropagation in two ways. First, we want derivative of network output not the loss function. Second, It is calculated w.r.t to input X rather than network parameters. I think this can be achieved in Tensorflow using tf.gradients(). How do I perform this op in PyTorch? I am not sure if I can use backward() function here.

Thanks

9 Likes
2

You can use torch.autograd.grad for stuff like this.

2 Likes
3

Hi, I think to this day the only way is to use grad function, but you will need to call it j times (once for each output). Unfortunately this requires many backward propagations and scales terribly with the output space of the function.

I have this exact same need, is there a different way to get the Jacobian of a function?

3 Likes
4

I came across a different solution which uses backward function. It’s all about playing with backward's parameters. More information can be found here. I am still looking for a better solution, if it exists.

1 Like
5

Thank you saan77, but I am still unable to understand how it is possible to get the Jacobian with a single backward pass.

The grad_tensors argument of backward seems to work as a weighting mask for the tensors argument in the thread you posted.

I don’t want the gradient of my tensors to be accumulated at leaf nodes. I want to get the gradient of each of my tensors with respect to leaf nodes. Let’s say I have an image classifier, whose input has shape (batchsize, c, h, w) and its output has shape (batchsize, n_classes), I want the jacobian to have shape (batchsize, c, h, w, n_classes).

Did you manage to get something similar?

6

Yes, you need to call it n times, where n is the number of output nodes. I am not sure if there is a way to compute this in a single pass. compute_jacobian function of this script computes jacobian using backward.

7

I have the exact same issue. I need to compute jacobian many times, and it’s terribly slow to have that many backward passes.

The python Autograd library is much better for jacobian. I was thinking if I could do the same with pytorch.

I hope they implement jacobian soon.

2 Likes
8

I guess it is related to “reverse-mode vs forward-mode”. As wikipedia Automatic_differentiation states, reverse-mode is more efficient for “tensor input scalar output” while forward-mode is more efficient for “scalar input tensor output”. That’s why machine learning library uses reverse-mode.

Jacobian matrix, however, is about “tensor input tensor output”. Not sure which way would be more efficient :thinking:.

2 Likes
9

The following code will do the trick with a single call to backward, taking advantage of when the function takes batched inputs.

6 Likes
10

Interesting, I think it only works with input vectors, I don’t see a way to extend it to parameter vectors.

1 Like
11

This (verbose) post may help to explain how to do the reconstruction.

“Because .backward() requires gradient arguments as inputs and performs a matrix multiplication internally to give the output (see eq 4), the way to obtain the Jacobian is by feeding in a gradient input which accounts for that specific row of the Jacobian. This is done by providing a mask for the specific dimension in the gradient vector”

1 Like
12

@Suzyahyah 's linked post is from July 2018. Is there a more recent post on computing the end-to-end Jacobian of a network in PyTorch?

13

This is the ticket for the forward-mode AD feature request
https://github.com/pytorch/pytorch/issues/10223 . This would enable more efficient Jacobian calculation.

2 Likes
14

Here are some functions that can help you.

import torch

def gradient(y, x, grad_outputs=None):
    """Compute dy/dx @ grad_outputs"""
    if grad_outputs is None:
        grad_outputs = torch.ones_like(y)
    grad = torch.autograd.grad(y, [x], grad_outputs = grad_outputs, create_graph=True)[0]
    return grad

def jacobian(y, x):
    """Compute dy/dx = dy/dx @ grad_outputs; 
    for grad_outputs in [1, 0, ..., 0], [0, 1, 0, ..., 0], ...., [0, ..., 0, 1]"""
    jac = torch.zeros(y.shape[0], x.shape[0]) 
    for i in range(y.shape[0]):
        grad_outputs = torch.zeros_like(y)
        grad_outputs[i] = 1
        jac[i] = gradient(y, x, grad_outputs = grad_outputs)
    return jac

def divergence(y, x):
    div = 0.
    for i in range(y.shape[-1]):
        div += torch.autograd.grad(y[..., i], x, torch.ones_like(y[..., i]), create_graph=True)[0][..., i:i+1]
    return div

def laplace(y, x):
    grad = gradient(y, x)
    return divergence(grad, x)

Illustration

x = torch.tensor([1., 2., 3.], requires_grad=True)
w = torch.tensor([[1., 2., 3.], [0., 1., -1.]])
b = torch.tensor([1., 2.])
y = torch.matmul(x, w.t()) + b # y = x @ wT + b => y1 = x1 + 2*x2 + 3*x3 + 1 = 15, y2 = x2 - x3 + 2 = 1
dydx = gradient(y, x)  # => jacobian(y, x) @ [1, 1]
jac = jacobian(y, x) 
div = divergence(y, x)
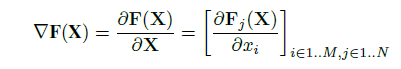
```
4 Likes
15

Hey folks I have some exciting news on this front. I was trying to solve the same problem but for a large network that will not work with batch. Even then the batch method described here is still very slow. Instead I devised a way that is highly efficient for network inputs that are relatively small (in my case a VAE decoder with 32 vector input). All you have to do is use a finite difference jacobian, and then the chainrule becomes completely unnecessary. My implementation is not general so I will not share it here (it’s also in C++ pytorch), but you can find an easy matlab version of finite difference jacobians that I based mine off of here from my wonderful math professors! Note that I had to tune the delta to work for the neural network since their matlab code is in double prec

1 Like
16

I was searching for a solution for the same problem and found out that Autograd now has a functional module that solves this exact problem. Specifically, torch.autograd.functional.jacobian, given a function and input variables, returns the Jacobian. There are also functions to compute the Hessian, Jacobian-vector-product, etc.

3 Likes
17

Hi,
I implemented the computation of the Jacobian matrix using the torch.autograd.functional.jacobian as below. However, it’s still too slow, please help me improve this.

def jacobianBatch(f, wrt):
    '''
    Compute the jacobian (derivaties of outputs w.r.t inputs)
    Input:
            f: pytorch model
            wrt: batch of training data
    Output:
            jacobian: J of the batch of training data
    '''
    jacobian = []
    f.eval()
    for i in range(wrt.shape[0]):
        jac = torch.autograd.functional.jacobian(f, wrt[i])
        jacobian.append(jac)
        #
    return torch.stack(jacobian, 0)
18

autograd.grad itself is a batch version. So if you use @pascal_notsawo method, you just need to iterate n times (n is your variable dimension rather than the batch dimension). So maybe if your variable dimension is smaller, you can iterate over that.