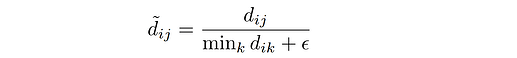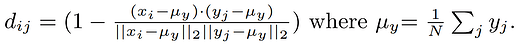I have two tensors x and y. I want to compute normalized cosine distance d_norm as follows
where
Assume that the term x_i - mu_y and y_j - mu_yreplaced by x_normalized and y_normalized, respectively. The d_norm can be computed as follows
N, C,H,W = x_normalized.size()
x_normalized = x_normalized.reshape(N, C, -1) # (N, C, H*W)
y_normalized = y_normalized.reshape(N, C, -1) # (N, C, H*W)
cosine_sim = torch.bmm(x_normalized.transpose(1, 2), y_normalized) # (N, H*W, H*W)
d = 1 - cosine_sim # (N, H*W, H*W) d[n, i, j] means d_ij for n-th data
d_min, _ = torch.min(d, dim=2, keepdim=True) # (N, H*W, 1)
d_norm = d / (d_min + 1e-5)
The above code works but it has one issue is that CUDA memory error when the size of x_normalized and y_normalized are big such as 256x256. That reason is due to the torch.bmm function. I am wonder do we have another way for batch multiplication as bmm did? If not, can we use the built-in function torch.nn.CosineSimilarity to compute the d_norm?
Thanks.
This is what I did using the pytorch built in function. However, two results are different.
cos sim: tensor(-6.5344e-05, grad_fn=<MeanBackward0>)
tensor(36834.2500, grad_fn=<MeanBackward0>)
Using pytorch function
cos sim: tensor(-0.0559, grad_fn=<MeanBackward0>)
tensor(0.9977, grad_fn=<MeanBackward0>)
To reproduce the result, you can use the code
import torch
import numpy as np
import torch.nn as nn
def cosine_dist(x, y, h=0.5):
assert x.size() == y.size()
N, C, H, W = x.size()
y_mu = y.mean(3).mean(2).mean(0).reshape(1, -1, 1, 1)
x_centered = x - y_mu
y_centered = y - y_mu
x_normalized = x_centered / torch.norm(x_centered, p=2, dim=1, keepdim=True)
y_normalized = y_centered / torch.norm(y_centered, p=2, dim=1, keepdim=True)
# The equation at the bottom of page 6 in the paper
# Vectorized computation of cosine similarity for each pair of x_i and y_j
x_normalized = x_normalized.reshape(N, C, -1) # (N, C, D*H*W)
y_normalized = y_normalized.reshape(N, C, -1) # (N, C, D*H*W)
cosine_sim = torch.bmm(x_normalized.transpose(1, 2), y_normalized) # (N, D*H*W, D*H*W)
print ('cos sim:', torch.mean(cosine_sim))
d = 1 - cosine_sim # (N, D*H*W, D*H*W) d[n, i, j] means d_ij for n-th data
d_min, _ = torch.min(d, dim=2, keepdim=True) # (N, D*H*W, 1)
d_norm = d / (d_min + 1e-5)
return d_norm
def cosine_dist_pytorch(x, y, h=0.5):
assert x.size() == y.size()
N, C, H, W = x.size()
y_mu = y.mean(3).mean(2).mean(0).reshape(1, -1, 1, 1)
x_centered = x - y_mu
y_centered = y - y_mu
x_normalized = x_centered / torch.norm(x_centered, p=2, dim=1, keepdim=True)
y_normalized = y_centered / torch.norm(y_centered, p=2, dim=1, keepdim=True)
x_normalized = x_normalized.reshape(N, C, -1) # (N, C, D*H*W)
y_normalized = y_normalized.reshape(N, C, -1) # (N, C, D*H*W)
#cosine_sim = torch.bmm(x_normalized.transpose(1, 2), y_normalized) # (N, D*H*W, D*H*W)
cos = nn.CosineSimilarity(dim=1, eps=1e-6)
cosine_sim = cos(x_normalized, y_normalized).unsqueeze_(2)
print ('cos sim:', torch.mean(cosine_sim))
d = 1 - cosine_sim # (N, D*H*W, D*H*W) d[n, i, j] means d_ij for n-th data
d_min, _ = torch.min(d, dim=2, keepdim=True) # (N, D*H*W, 1)
d_norm = d / (d_min + 1e-5)
return d_norm
img1 = torch.rand((4, 2, 16, 16), requires_grad=True)
img2 = torch.rand((4, 2, 16, 16), requires_grad=True)
loss1 = cosine_dist(img1, img2)
print (torch.mean(loss1))
print ('\nUsing pytorch function')
loss2 = cosine_dist_pytorch(img1, img2)
print (torch.mean(loss2))