How to Create Upper Triangular Matrix with Diagonals of Increasing Power?

1

I’d like to create a square upper triangular matrix that is defined as follows for some float c and some dimension N:

[[1 , c , c^2, ... c^N],
 [0,  1 ,   c, ... c^{N-1}],
 [0,  0 ,   1, ... c^{N-2}],
 .
 .
 .
 [0,  0 ,   0, ....    1]]

For concreteness, if N=2, then the matrix should be

[[1, c],
 [0, 1]]

And if N=3, then the matrix should be:


[[1, c, c^2],
 [0, 1,   c],
 [0, 0,   1]]

How can I do this?

2

Right now I’m doing the following. Is there a faster way?

            discount_matrix = torch.triu(torch.ones(
                size=(N, N)))
            for i in range(1, N):
                tril_idx = torch.triu_indices(
                    row=N,
                    col=N,
                    offset=i)
                discount_matrix[tril_idx[0], tril_idx[1]] *= c
3

The Python loop wouldn’t scale that well for larger values of N.
You could use an approach of repeating the initial tensor and calling view on it to create an “interleaved” tensor. This approach would be a bit wasteful in memory, but would yield a better compute performance.

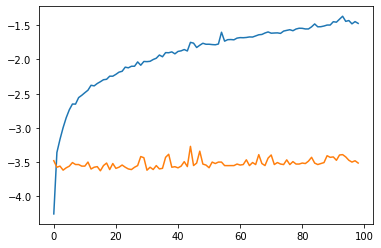
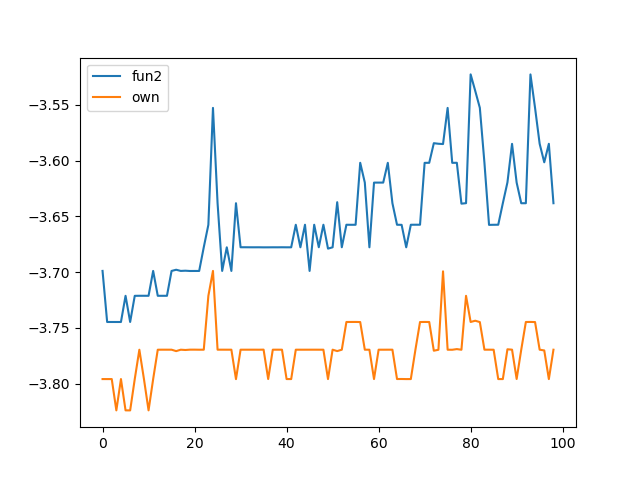
Here is the comparison with a quick profiling for CPU and GPU:

def fun1(N, c, device):
    discount_matrix = torch.triu(torch.ones(size=(N, N), device=device))
    for i in range(1, N):
        tril_idx = torch.triu_indices(
            row=N,
            col=N,
            offset=i)
        discount_matrix[tril_idx[0], tril_idx[1]] *= c
    return discount_matrix
    

def fun2(N, c, device):
    tmp = torch.tensor([float(c)**i for i in range(N)], device=device)
    tmp = torch.cat((tmp, torch.zeros(1, device=device)))
    res = torch.triu(tmp.repeat(N).view(-1, N)[:-1])
    return res


c = 2
nb_iters = 100

f1_times = []
f2_times = []

device = 'cuda'

for N in range(1, 100):
    # correctness check
    print((fun1(N, c, device) == fun2(N, c, device)).all())
    
    # timing
    torch.cuda.synchronize()
    t0 = time.time()
    for _ in range(nb_iters):
        out = fun1(N, c, device)
    torch.cuda.synchronize()
    t1 = time.time()
    f1_time = (t1 - t0)/nb_iters
    print('fun1({}, {}): {}ms'.format(N, c, f1_time))
    f1_times.append(f1_time)
    
    torch.cuda.synchronize()
    t0 = time.time()
    for _ in range(nb_iters): 
        out = fun2(N, c, device)
    torch.cuda.synchronize()
    t1 = time.time()
    f2_time = (t1 - t0)/nb_iters
    print('fun2({}, {}): {}ms'.format(N, c, f2_time))
    f2_times.append(f2_time)


plt.figure()
plt.plot(np.log10(np.array(f1_times)))
plt.plot(np.log10(np.array(f2_times)))

Results for N in range(1, 100). Blue curve: your approach, orange curve: my proposal, y-axis: log10 of the time in ms, x-axis: N (sorry for being too lazy to properly add the legends into the plot :wink: ).

CPU:
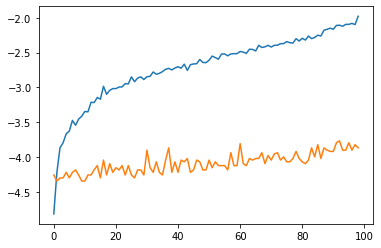
image

GPU:
image

4

I just encountered the same problem and wanted to share my approach.

def fun3(N, c, device):
    exponents = torch.triu(torch.ones(N, N, device=device), 1).cumsum(-1)
    power = torch.float_power(c, exponents)
    power_mask = torch.tril(torch.ones(N, N, dtype=torch.bool, device=device), diagonal=-1)
    result = power.masked_fill(power_mask, 0)
    return result

Avoiding the for-loops seems to be a little bit more performant (tested with GPU):

grafik

If anyone wants to replicate my results, you’ll have to adjust the correctness check a little:

assert torch.isclose(fun2(N, c, device).double(), fun3(N, c, device)).all()
1 Like