I am currently implementing WGAN using weight clipping for a dataset of 3x256x256 images. I’ve taken a working implementation of DCGAN for the same dataset and have converted to to WGAN by removing the sigmoid from the discriminator and changing the loss function.
The issue is that the Critic loss decreases steadily and stabilizes around -6 very quickly, and the Generator loss increases and stabilizes around 3 very quickly. It also seems like the gradients in the Generator vanish as training progresses leading to very poor image quality.
I’ve experimented by increasing the learning rate, increasing the critic training iterations, and changing the form of normalization in the Critic from BatchNorm, LayerNorm, to no normalization at all. I also tried to increase the clamping parameter with hopes of minimizing the vanishing gradients problem but to no avail.
Interestingly with no normalization, the Critic loss does tend to zero (though it fluctuates wildly around this point within ±50k) but the losses become very large (to the scale of 1e9). The image quality is still very poor.
Are there any ways I can go about debugging this? Alternatively is there something fundamentally wrong with my implementation? I’ve attached some code below:
Generator(
(network): ModuleList(
(0): Sequential(
(0): ConvTranspose2d(100, 2048, kernel_size=(4, 4), stride=(1, 1), bias=False)
(1): BatchNorm2d(2048, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): LeakyReLU(negative_slope=0.2, inplace=True)
)
(1): Sequential(
(0): ConvTranspose2d(2048, 1024, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(1): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): LeakyReLU(negative_slope=0.2, inplace=True)
)
(2): Sequential(
(0): ConvTranspose2d(1024, 512, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): LeakyReLU(negative_slope=0.2, inplace=True)
)
(3): Sequential(
(0): ConvTranspose2d(512, 256, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): LeakyReLU(negative_slope=0.2, inplace=True)
)
(4): Sequential(
(0): ConvTranspose2d(256, 128, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): LeakyReLU(negative_slope=0.2, inplace=True)
)
(5): Sequential(
(0): ConvTranspose2d(128, 64, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): LeakyReLU(negative_slope=0.2, inplace=True)
)
(6): Sequential(
(0): ConvTranspose2d(64, 3, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(1): Tanh()
)
)
)
Critic(
(network): ModuleList(
(0): Sequential(
(0): Conv2d(3, 64, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(1): LeakyReLU(negative_slope=0.2, inplace=True)
)
(1): Sequential(
(0): Conv2d(64, 128, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(1): GroupNorm(1, 128, eps=1e-05, affine=True)
(2): LeakyReLU(negative_slope=0.2, inplace=True)
)
(2): Sequential(
(0): Conv2d(128, 256, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(1): GroupNorm(1, 256, eps=1e-05, affine=True)
(2): LeakyReLU(negative_slope=0.2, inplace=True)
)
(3): Sequential(
(0): Conv2d(256, 512, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(1): GroupNorm(1, 512, eps=1e-05, affine=True)
(2): LeakyReLU(negative_slope=0.2, inplace=True)
)
(4): Sequential(
(0): Conv2d(512, 1024, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(1): GroupNorm(1, 1024, eps=1e-05, affine=True)
(2): LeakyReLU(negative_slope=0.2, inplace=True)
)
(5): Sequential(
(0): Conv2d(1024, 2048, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
(1): GroupNorm(1, 2048, eps=1e-05, affine=True)
(2): LeakyReLU(negative_slope=0.2, inplace=True)
)
(6): Sequential(
(0): Conv2d(2048, 1, kernel_size=(4, 4), stride=(1, 1), bias=False)
)
)
)
Training Loop:
# Training Loop - adapted directly from DCGAN tutorial
#hyper params
z_dim = 100
lr = 5e-5
c = 0.01 #clamping parameter
n_critic = 20 # critic training iterations
S = 500 # sampling interval
# Lists to keep track of progress
img_list = []
G_losses = []
D_losses = []
iters = 0
num_epochs = 250
torch.autograd.set_detect_anomaly(True)
print("Starting Training Loop...")
print(device)
# For each epoch
for epoch in range(num_epochs):
# For each batch in the dataloader
for i, data in enumerate(dataloader, 0):
#train critic
netD.zero_grad()
# Format batch
real_cpu = data[0].to(device)
b_size = real_cpu.size(0)
#label = torch.full((b_size,), real_label, dtype=torch.float, device=device)
# Forward pass real batch through D
#add decaying noise to real input
real_input = real_cpu #+ ( torch.randn(real_cpu.size(), device=device) + mu ) * (std/(epoch+1))
output_real = netD(real_input).view(-1)
# Forward pass fake batch through D
# Generate batch of latent vectors
noise = torch.randn(b_size, z_dim, 1, 1, device=device)
# Generate fake image batch with G
fake = netG(noise)
#f_label = torch.full((b_size,), fake_label, dtype=torch.float, device=device)#.fill_(fake_label)
# Classify all fake batch with D
fake_input = fake
output_fake = netD(fake_input.detach()).view(-1)
# Add the gradients from the all-real and all-fake batches
errD = -(torch.mean(output_real) - torch.mean(output_fake))
errD.backward()
optimizerD.step()
#clamp critic weights
for p in netD.parameters():
p.data.clamp_(-c,c)
#train generator
if i % n_critic == 0:
netG.zero_grad()
#label.fill_(real_label) # fake labels are real for generator cost
# Since we just updated D, perform another forward pass of all-fake batch through D
output = netD(fake_input).view(-1)
# Calculate G's loss based on this output
errG = -torch.mean(output)
# Calculate gradients for G
errG.backward()
# Update G
optimizerG.step()
# Output training stats
print('[%d/%d][%d/%d]\tLoss_D: %.4f\tLoss_G: %.4f'
% (epoch, num_epochs, i, len(dataloader),
errD.item(), errG.item()))
# Save Losses for plotting later
G_losses.append(errG.item())
D_losses.append(errD.item())
#plot gradient flow of generator
if iters == 10 or iters == 50 or iters % S == 0:
plot_grad_flow(netG.named_parameters())
# Check how the generator is doing by saving G's output on fixed_noise
if (iters % S == 0) or ((epoch == num_epochs-1) and (i == len(dataloader)-1)):
with torch.no_grad():
fake = netG(fixed_noise).detach().cpu()
img_list.append(vutils.make_grid(fake, padding=2, normalize=True))
iters += 1
This is what the typical loss graph looks like:
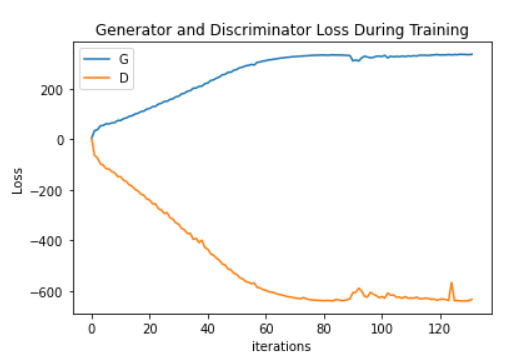
Usually it is more smoothly curved on its path, this particular graph came from setting c=0.1
At this point I am suspicious of an error in my implementation. Can anyone suggest to me any possible errors I have made?