I am new to Pytorch so pardon if the question sounds stupid.
I am trying to do some sort of reinforcement learning similar to “http://karpathy.github.io/2016/05/31/rl/”.
An agent needs to choose either “up” or “down” based on the inputs. As mentioned in the link, uppon winning the game, I assign “1” and “0” as errors to “up” and “down”, respectively, otherwise, “0” and “-1”, and backpropagate the error.
The problem is, in all pytorch c++ examples, i just see that the mean or sum of the errors (loss) is backpropagated. So my question is, how can I backpropagate for each loss defined for each output item?
Hi,
You will need to run as many backwards as gradients you want unfortunately.
The nice thing with sum/avg is that since you want a single gradient, you can compute them at once.
That being said, if your network has some special structure, you might be able to use tricks like this one to do it: https://github.com/cybertronai/autograd-hacks
Can you help me to understand how repeating backwards would help? Assuming that I have the loss as either [1,0] or [0,-1], how can I use backwards() as it only works for a scalar loss? thanks
how can I backpropagate for each loss defined for each output item?
Simply call backward for each of them: output[i].backward(your_error) ?
as a minimal example, is this what you suggest?
struct Net : torch::nn::Module {
Net() {
fc1 = register_module("fc1", torch::nn::Linear(1, 3));
fc2 = register_module("fc2", torch::nn::Linear(3, 4));
fc3 = register_module("fc3", torch::nn::Linear(4, 2));
}
// Implement the Net's algorithm.
torch::Tensor forward(torch::Tensor x) {
x = torch::sigmoid(fc1->forward(x));
x = torch::dropout(x, /*p=*/0.5, /*train=*/is_training());
x = torch::sigmoid(fc2->forward(x));
x = torch::log_softmax(fc3->forward(x), /*dim=*/1);
return x;
}
int main(){
auto net = std::make_shared<Net>();
torch::optim::SGD optimizer(net->parameters(), /*lr=*/0.01);
for (int ii=0; ii<100; ii++) {
optimizer.zero_grad();
auto inputs = generate_data(); // doesnt matter the values
torch::Tensor prediction = net->forward(inputs);
torch::Tensor loss =calculate_loss(prediction); // e.g. loss = [1,0]
for (auto item:loss){
item.backward();
}
optimizer.step();
}
If you do this, then the gradient from every backward call will be accumulated in the .grad field. Another way to get the same result is to sum your loss and backward the result.
as i understand, doing this:
for (auto item:loss){
item.backward();
}
or
loss.sum().backward()
should have more or less the same results. But neither is what i have in mind.
For example, if the errors are [1,0], by doing loss.sum().backward(), i am encouraging the whole system by 1, which is not my intention. What I want to do is to backpropagate 1 from the first output and 0 from the second output
Sorry I’m not sure to understand what you want to do here.
Could you write down mathematically what are the gradients you want to obtain?
OK. I prepared some stuff that could help.
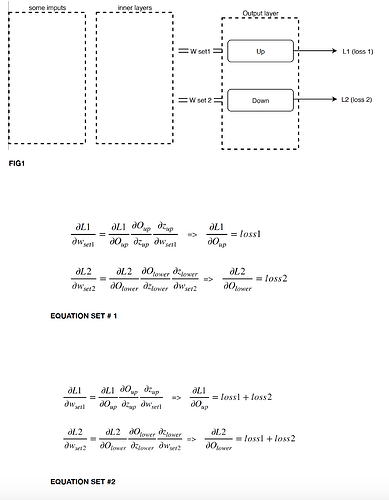
lets assume that FIG1 is my network with two outputs and corresponding errors, i.e. [loss1, loss2].
I can write the gradients for each output separately as EQUATION SET#1.
Basically, what is different for them is the value of the loss, i.e. loss 1 for ‘up’ and loss 2 for ‘down’.
This differs from the case we go with sum (or mean) that would result in EQUATION SET#2.
So my question is, how can I use Pytorch to implement the former but not latter?
And is w_{set1} used when computing L2 ? And w_{set2} when computing L1?
From your Equation set 1 they look independent. Is that the case?
yes they are independent. “up” and “down” are the output nodes so weights coming to each of them are different
If they are independent, then dL1/dw_{set2} = 0. So if you use L1 + L2, the gradient you compute for set2 for example are: d(L1+L2)/dw_{set2} = dL1/dw_{set2} + dL2/dw_{set2} = 0 + dL2/dw_{set2} = dL2/dw_{set2} which is what you want. And same thing for the gradients wrt w_{set1}
I was trying to verify what you just said that I came to something unexpected.
I have a dummy example of a 1*2 network without the inner layer. I compute the loss based on the first node of the output. As a result, the gradient on the second node is zero as the code also shows correctly. However, when I check the gradients on the weights, I can see non-zero values for the second row, which I expected to be zeros. How does this happen? if the gradient on a node is zero, shouldn’t the weights coming to that node also have zero gradients?
import torch
from torch import optim
#### network ####
class Net(torch.nn.Module):
def __init__(self, N, M):
super(Net, self).__init__()
self.fc1 = torch.nn.Linear(N, M)
def forward(self, x):
x = torch.softmax(self.fc1(x),1)
return x
nn = Net(1,2)
optimizer = optim.Adam(nn.parameters(), lr=0.01)
xx = torch.ones((1,1),requires_grad = True)
ys = nn.forward(xx)
ys.register_hook(print)
loss = abs(ys[0][0]-0.5)
optimizer.zero_grad()
loss.backward()
print(nn.fc1.weight.grad)
optimizer.step()
output:
Gradients on the output nodes:
tensor([[-1., 0.]])
Gradients on the weights:
tensor([[-0.1939],
[ 0.1939]])
Hi,
I think the prints don’t match your code. In particular, I’m not sure where the Gradients on the output nodes: comes from.
But to answer your question, this is most likely the softmax that makes the gradients dense even though they are sparse on its output (it’s actually a very useful feature of softmax!).
Thanks. It was because of softmax.
What i have learned as a newbie in pytorch is as follow:
If I have L1 and L2 as loss values for two different output nodes, I can simply do L = mean(L1,L2) and then L.backward(). But the trick is, since, in reinforcement learning (RL), the target value is not calculated based on NN output nodes, first we need to associate loss/reward to output nodes. To do so, in this example, doing (L1+ys[0][0].detach() - ys[0][0]) would keep the value of error still L1 but would make it connect to “ys”, so doing backward() would indeed adjust weights.
Similar approach is also taken in classic RL. Once we calculate reward R, it needs to be applied to the probability of chosen action. So, if we have output values as a tensor ys = [y1, y2], and assuming that agent has chosen the first output in this episode, i.e. [1,0], the loss function would be [y1,y2].*[1,0].*R, which connects R (which doesn’t have gradients) to ys (which has grads).
Hope this is helpful