How to implement a new function and its gradient in PyTorch?

autograd
1

I want to implement a function that cannot be easily expressed with functions already implemented in PyTorch. However, I know how to compute this function and its gradients numerically. How could I implement this function as something that plays nicely with other PyTorch functions?

2

I think that this is too general to answer.
The general answer would be to try and make a workaround using Pytorch functions.
If this is not possible then maybe you can look into defining your own autograd function. Here is an example on how to do this.

Here is a little more information on this.

Maybe you can post the equation or explain how this function should behave and maybe someone can come up with a solution or at least help you get in the right direction.

3

I am curious: Is there a way to see the gradients for the already implemented functions?

4

The backward formulae for basic PyTorch ops are defined in C++ source code which you can view on github, I don’t believe it’s accessible within the python API. If you want to define a new gradient do what @Matias_Vasquez already stated and use torch.autograd.Function to define a custom function.

5

Additionally to what @AlphaBetaGamma96 said, you could plot the gradients to visually inspect them by doing something like this.

def func(x):
    return torch.nn.ReLU()(4*x**2 - 2)-1
    
x = torch.arange(-2, 2.01, 0.01, requires_grad=True)

y = func(x)
y.backward(gradient=torch.ones_like(x))

y_prime = x.grad

plt.plot(x.detach().numpy(), y.detach().numpy(), label="y")
plt.plot(x.detach().numpy(), y_prime.numpy(), label="y'")
plt.legend()
plt.show()

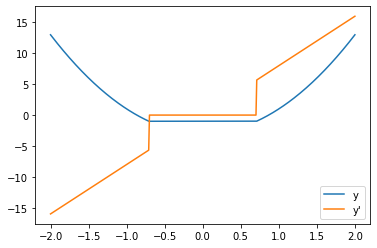
image

But this might only make sense for some functions. Others are just going to seem random noise.

# Using the same code as above, only changing the function
def func(x):
    return torch.nn.Linear(x.shape[-1], x.shape[-1])(x)

The result might look something like this ↓
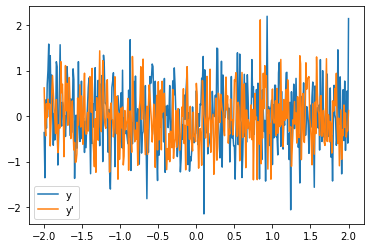
image

6

If you could share more about your use case, it would help clarify the situation.

Using torch.autograd.Function is good to define custom functions, but it can get messy very quickly as you have to manually define the backward component of your function.