Hi,
I am assuming that by looking for a differentiable solution, you mean that the resulting tensor has require_grad = True in the end. If so, then we have a problem because you want a boolean tensor.
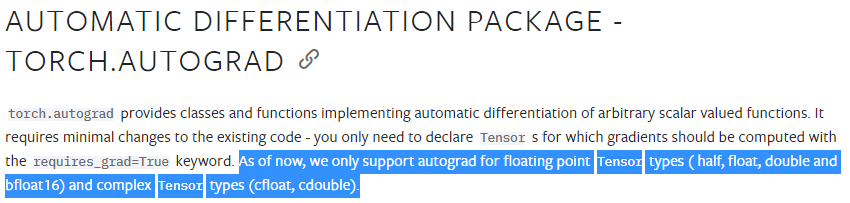
If we look at the documentation for autograd we can see that only floating point tensors are supported.
If this is the case, then I don´t think it is going to be possible to get what you want (a differentiable boolean tensor).
However, let me try and fail with extra steps:
Assuming
- You don´t care that
relevance_map is a dict
We can change it into a tensor, such that all end nodes have the same size. For this, I added -inf where the vectors are too short.
cartesian_prod = torch.tensor([[0., 9], [0, 5], [0, 7], [1, 9], [1, 5], [1, 7], [2, 9], [2, 5], [2, 7]], requires_grad=True)
relevance_map = torch.tensor([[5,9],[-float('inf'), 9],[5,7]])
Solution 1 - no grad
We get a boolean tensor, however, grad is lost when we do the equal (==) operation. If this was not the case, any will also remove it.
tmp = torch.any(relevance_map[cartesian_prod[:, 0].long()] == cartesian_prod[:, 1].unsqueeze(0).T, dim=1)
print(tmp)
print(tmp.requires_grad)
# tensor([ True, True, False, True, False, False, False, True, True])
# False
Solution 2 - not boolean (and weird format)
Here all opperations should be differentiable. The problem is that the output is a float tensor, where 0 means True and anything other than 0 is False. (as I said, weird format)
tmp2, _ = torch.abs(relevance_map[cartesian_prod[:, 0].long()] - cartesian_prod[:, 1].unsqueeze(0).T).min(dim=1)
print(tmp2)
print(tmp2.requires_grad)
# tensor([0., 0., 2., 0., 4., 2., 2., 0., 0.], grad_fn=<MinBackward0>)
# True
Solution 3 - even more unnecessary steps - still no boolean
Using tmp2 from the last solution.
Here 1 means True and 0 is False. (that´s better)
div = tmp2.clone()
div[div==0] = 1
tmp3 = -torch.div(tmp2, div) + 1
print(tmp3)
print(tmp3.requires_grad)
tensor([1., 1., 0., 1., 0., 0., 0., 1., 1.], grad_fn=<AddBackward0>)
True