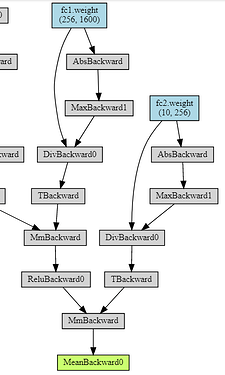
I’d like to train a convnet where each layer weights are divided by the maximum weight in that layer, at the start of every forward pass. So the range of the weights would always be [-1, 1].
I tried doing it like this:
class TestConv2d(nn.Conv2d):
def __init__(self, in_channels, out_channels, kernel_size=5, bias=False):
super(TestConv2d, self).__init__(in_channels, out_channels, kernel_size, bias=bias)
def forward(self, inputs):
return F.conv2d(inputs, self.weight / torch.max(torch.abs(self.weight)), self.bias)
class TestLinear(nn.Linear):
def __init__(self, in_features, out_features, bias=False):
super(TestLinear, self).__init__(in_features, out_features, bias=bias)
def forward(self, inputs):
return F.linear(inputs, self.weight / torch.max(torch.abs(self.weight)), self.bias)
class ConvNet(nn.Module):
def __init__(self):
super(ConvNet, self).__init__()
self.conv1 = TestConv2d(3, 32, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = TestConv2d(32, 64, 5)
self.flatten = nn.Flatten(start_dim=1)
self.fc1 = TestLinear(64 * 5 * 5, 390)
self.fc2 = TestLinear(256, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = self.flatten(x)
x = F.relu(self.fc1(x))
x = self.fc2(x)
return x
The rest of the code is a standard training loop, and it works as expected on CIFAR-10 without weights scaling.
With weight scaling, however, there is some weird behavior. I tried training it with SGD and AdamW, and AdamW works much better. I had to reduce the initial learning rate significantly (compared to no scaling scanario), especially with SGD. However, I’m still not able to reach the same accuracy as without weight scaling (~2% drop with AdamW, ~10% drop with SGD).
Questions:
- What is happening to the weight gradients when I’m modifying weights like this?
- What would be a correct way to implement weight scaling?
- Why is AdamW works so much better than SGD in this case?