I was trying to train a simple polynomial linear regression model in pytorch with SGD. I wrote some self contained (what I thought would be extremely simple code), however, for some reason my model does not train as I thought it should.
I have 5 points sampled from a sine curve and try to fit it with a polynomial of degree 4. This is a convex problem so GD or SGD should find a solution with zero train error eventually as long as we have enough iterations and small enough step size. For some reason however my model does not train well (even though it seems that it is changing the parameters of the model. Anyone have an idea why? Here is the code (I tried making it self contained and minimal):
import numpy as np
from sklearn.preprocessing import PolynomialFeatures
import torch
from torch.autograd import Variable
from maps import NamedDict
from plotting_utils import *
def index_batch(X,batch_indices,dtype):
'''
returns the batch indexed/sliced batch
'''
if len(X.shape) == 1: # i.e. dimension (M,) just a vector
batch_xs = torch.FloatTensor(X[batch_indices]).type(dtype)
else:
batch_xs = torch.FloatTensor(X[batch_indices,:]).type(dtype)
return batch_xs
def get_batch2(X,Y,M,dtype):
'''
get batch for pytorch model
'''
# TODO fix and make it nicer, there is pytorch forum question
X,Y = X.data.numpy(), Y.data.numpy()
N = len(Y)
valid_indices = np.array( range(N) )
batch_indices = np.random.choice(valid_indices,size=M,replace=False)
batch_xs = index_batch(X,batch_indices,dtype)
batch_ys = index_batch(Y,batch_indices,dtype)
return Variable(batch_xs, requires_grad=False), Variable(batch_ys, requires_grad=False)
def get_sequential_lifted_mdl(nb_monomials,D_out, bias=False):
return torch.nn.Sequential(torch.nn.Linear(nb_monomials,D_out,bias=bias))
def train_SGD(mdl, M,eta,nb_iter,logging_freq ,dtype, X_train,Y_train):
##
N_train,_ = tuple( X_train.size() )
#print(N_train)
for i in range(nb_iter):
# Forward pass: compute predicted Y using operations on Variables
batch_xs, batch_ys = get_batch2(X_train,Y_train,M,dtype) # [M, D], [M, 1]
## FORWARD PASS
y_pred = mdl.forward(batch_xs)
## LOSS + Regularization
batch_loss = (1/M)*(y_pred - batch_ys).pow(2).sum()
## BACKARD PASS
batch_loss.backward() # Use autograd to compute the backward pass. Now w will have gradients
## SGD update
for W in mdl.parameters():
delta = eta*W.grad.data
W.data.copy_(W.data - delta)
## train stats
if i % (nb_iter/10) == 0 or i == 0:
current_train_loss = (1/N_train)*(mdl.forward(X_train) - Y_train).pow(2).sum().data.numpy()
print('i = {}, current_loss = {}'.format(i, current_train_loss ) )
## Manually zero the gradients after updating weights
mdl.zero_grad()
##
logging_freq = 100
dtype = torch.FloatTensor
## SGD params
M = 3
eta = 0.0002
nb_iter = 20*1000
##
lb,ub = 0,1
f_target = lambda x: np.sin(2*np.pi*x)
N_train = 5
X_train = np.linspace(lb,ub,N_train)
Y_train = f_target(X_train)
## degree of mdl
Degree_mdl = 4
## pseudo-inverse solution
c_pinv = np.polyfit( X_train, Y_train , Degree_mdl )[::-1]
## linear mdl to train with SGD
nb_terms = c_pinv.shape[0]
mdl_sgd = get_sequential_lifted_mdl(nb_monomials=nb_terms,D_out=1, bias=False)
## Make polynomial Kernel
poly_feat = PolynomialFeatures(degree=Degree_mdl)
Kern_train = poly_feat.fit_transform(X_train.reshape(N_train,1))
Kern_train_pt, Y_train_pt = Variable(torch.FloatTensor(Kern_train).type(dtype), requires_grad=False), Variable(torch.FloatTensor(Y_train).type(dtype), requires_grad=False)
train_SGD(mdl_sgd, M,eta,nb_iter,logging_freq ,dtype, Kern_train_pt,Y_train_pt)
the error seems to hover on 2ish:
i = 0, current_loss = [ 2.08996224]
i = 2000, current_loss = [ 2.03536892]
i = 4000, current_loss = [ 2.02014995]
i = 6000, current_loss = [ 2.01307297]
i = 8000, current_loss = [ 2.01300406]
i = 10000, current_loss = [ 2.01125693]
i = 12000, current_loss = [ 2.01162267]
i = 14000, current_loss = [ 2.01296973]
i = 16000, current_loss = [ 2.00951076]
i = 18000, current_loss = [ 2.00967121]
which is weird cuz it should be able to reach zero.
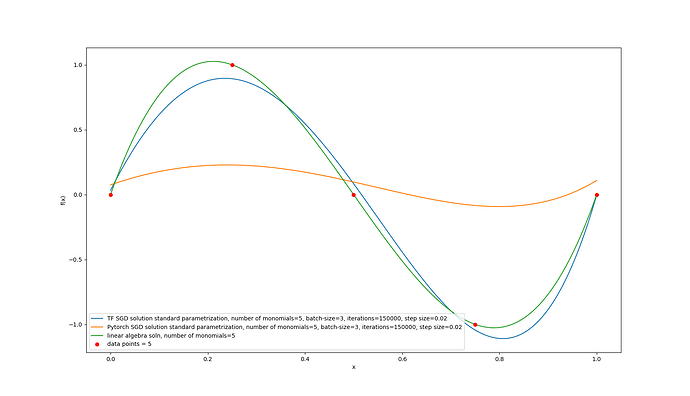
I also plotted the learned function:
the code for the plotting:
##
x_horizontal = np.linspace(lb,ub,1000).reshape(1000,1)
X_plot = poly_feat.fit_transform(x_horizontal)
X_plot_pytorch = Variable( torch.FloatTensor(X_plot), requires_grad=False)
##
fig1 = plt.figure()
#plots objs
p_sgd, = plt.plot(x_horizontal, [ float(f_val) for f_val in mdl_sgd.forward(X_plot_pytorch).data.numpy() ])
p_pinv, = plt.plot(x_horizontal, np.dot(X_plot,c_pinv))
p_data, = plt.plot(X_train,Y_train,'ro')
## legend
nb_terms = c_pinv.shape[0]
legend_mdl = f'SGD solution standard parametrization, number of monomials={nb_terms}, batch-size={M}, iterations={nb_iter}, step size={eta}'
plt.legend(
[p_sgd,p_pinv,p_data],
[legend_mdl,f'linear algebra soln, number of monomials={nb_terms}',f'data points = {N_train}']
)
##
plt.xlabel('x'), plt.ylabel('f(x)')
plt.show()
I actually went ahead and implemented a TensorFlow version. That one does seem to train the model. I tried having both of them match by giving them the same initialization:
mdl_sgd[0].weight.data.fill_(0)
but that still didn’t work. Tensorflow code:
graph = tf.Graph()
with graph.as_default():
X = tf.placeholder(tf.float32, [None, nb_terms])
Y = tf.placeholder(tf.float32, [None,1])
w = tf.Variable( tf.zeros([nb_terms,1]) )
#w = tf.Variable( tf.truncated_normal([Degree_mdl,1],mean=0.0,stddev=1.0) )
#w = tf.Variable( 1000*tf.ones([Degree_mdl,1]) )
##
f = tf.matmul(X,w) # [N,1] = [N,D] x [D,1]
#loss = tf.reduce_sum(tf.square(Y - f))
loss = tf.reduce_sum( tf.reduce_mean(tf.square(Y-f), 0))
l2loss_tf = (1/N_train)*2*tf.nn.l2_loss(Y-f)
##
learning_rate = eta
#global_step = tf.Variable(0, trainable=False)
#learning_rate = tf.train.exponential_decay(learning_rate=eta, global_step=global_step,decay_steps=nb_iter/2, decay_rate=1, staircase=True)
train_step = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(loss)
with tf.Session(graph=graph) as sess:
Y_train = Y_train.reshape(N_train,1)
tf.global_variables_initializer().run()
# Train
for i in range(nb_iter):
#if i % (nb_iter/10) == 0:
if i % (nb_iter/10) == 0 or i == 0:
current_loss = sess.run(fetches=loss, feed_dict={X: Kern_train, Y: Y_train})
print(f'i = {i}, current_loss = {current_loss}')
## train
batch_xs, batch_ys = get_batch(Kern_train,Y_train,M)
sess.run(train_step, feed_dict={X: batch_xs, Y: batch_ys})
I also tried changing the initialization but it didn’t change anything, which makes sense cuz it shouldn’t make a big difference:
mdl_sgd[0].weight.data.normal_(mean=0,std=0.001)
post on SO: python - How to train a simple linear regression model with SGD in pytorch successfully? - Stack Overflow
I even implemented it in tensorflow and that version of the code does work! Since the model does approach the linear algebra solution: