Saying that I have a layer feature map output of the form (1,1,10,10) how can I transform it to (4,1,5,5), while keeping the spatial location as a kernel of 5x5 as mentioned in the image bellow and preserving the gradient ?
As you can see, the features are moved to form new inputs in the input channel.
Why don’t you just slice the tensor and then stack it?
Something like:
orange = X[0,:,:X.size(2)//2,:X.size(3)//2]
blue = X[0,:,:X.size(2)//2,X.size(3)//2:]
grey = X[0,:,X.size(2)//2:,:X.size(3)//2]
green = X[0,:,X.size(2)//2:,X.size(3)//2:]
output = torch.stack([orange,blue,grey,green])
This should preserve the gradients I believe.
this could work if I have only one input what if I have (4,1,10,10) to be (16,1,5,5) or what if I have (4,1,20,20) to be (64,1,5,5) ? I’m looking for an automatic function that takes a kernel of 5 by 5 and stake it in the first channel of the tensor
You could adapt the slicing method to any size just by putting it in a for loop or calling it recursively. You could also do it with a “kernel” by using a a 2d Convolution with weights set to the identity, and then reshape them to be a square again. This method I’d say is a bit more tricky, and you’d need to work out the correct stride sizes for the convolution.
Making a loop in a large input image is very costly process. Could you elaborate more please about using a 2d conv?
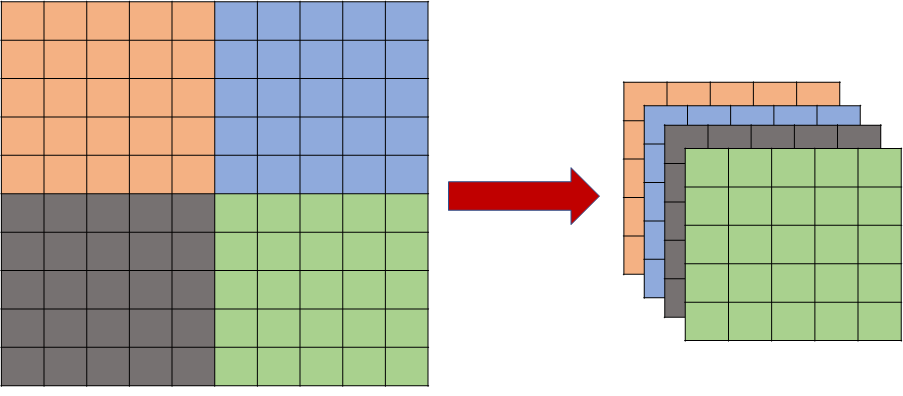
So a convolution2d operator is essentially a simple matrix multiplication over a flattened patch of an image. If your entire image is [b,1,10,10] and you choose convolution with kernel W of size (5,5) with output size (d) and with stride=5, it will do the following 4 operations, say the output is O of size [b,d,2,2]:
O[b_i,0:d,0,0] = W * X[b_i,:,:5,:5].view(1*5*5) where W is size (d,1x5x5)
O[b_i,0:d,0,1] = W * X[b_i,:,:5,5:].view(1*5*5)
etc.
So if you set output dimension to same as input dimension (d = 1x5x5) and set it to Identity matrix it will preserve all the information. And you can then reshape it back into (5,5) and have the same image.
So your output O is of size (b,1x5x5,2,2). Flatten last two dimensions -> (b,5x5,4). Then transpose -> (b,4,5x5). Then reshape again -> (b,4,5,5), and voila.
But slicing much less confusing, not sure about the speed of this vs the for loop with slicing.
